题目内容
【题目】已知函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() <φ<
<φ< ![]() )的部分图象如图所示;
)的部分图象如图所示; 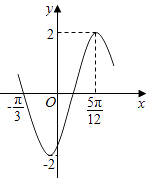
(1)求ω,φ;
(2)将y=f(x)的图象向左平移θ(θ>0)个单位长度,得到y=g(x)的图象,若y=g(x)图象的一个对称点为( ![]() ,0),求θ的最小值.
,0),求θ的最小值.
(3)对任意的x∈[ ![]() ,
, ![]() ]时,方程f(x)=m有两个不等根,求m的取值范围.
]时,方程f(x)=m有两个不等根,求m的取值范围.
【答案】
(1)解:根据函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() <φ<
<φ< ![]() )的部分图象,可得
)的部分图象,可得 ![]()
![]() =
= ![]() ,
,
求得ω=2.
再根据五点法作图可得2 ![]() +φ=
+φ= ![]() ,求得φ=﹣
,求得φ=﹣ ![]() ,∴f(x)=2sin(2x﹣
,∴f(x)=2sin(2x﹣ ![]() )
)
(2)解:将y=f(x)的图象向左平移θ(θ>0)个单位长度,得到y=g(x)=2sin[2(x+θ)﹣ ![]() ]=2sin(2x+2θ﹣
]=2sin(2x+2θ﹣ ![]() )的图象,
)的图象,
∵y=g(x)图象的一个对称点为( ![]() ,0),∴2
,0),∴2 ![]() +2θ﹣
+2θ﹣ ![]() =kπ,k∈Z,∴θ=
=kπ,k∈Z,∴θ= ![]() ﹣
﹣ ![]() ,故θ的最小正值为
,故θ的最小正值为 ![]()
(3)解:对任意的x∈[ ![]() ,
, ![]() ]时,2x﹣
]时,2x﹣ ![]() ∈[
∈[ ![]() ,
, ![]() ],sin(2x﹣
],sin(2x﹣ ![]() )∈[﹣
)∈[﹣ ![]() ,1],即f(x)∈[﹣
,1],即f(x)∈[﹣ ![]() ,2],
,2],
∵方程f(x)=m有两个不等根,结合函数f(x),x∈[ ![]() ,
, ![]() ]时的图象可得,1≤m<2.
]时的图象可得,1≤m<2.
【解析】(1)用五点法做函数y=Asin(ωx+φ)在一个周期上的简图.(2)利用y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,求得θ的最小正值.(3)利用正弦函数的定义域和值域,结合函数f(x)的图象,求得m的取值范围.
【考点精析】认真审题,首先需要了解函数y=Asin(ωx+φ)的图象变换(图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象).
的图象).

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800 名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100 分)进行统计,得到如下的频率分布表,请你根据频率分布表解答下列问题:
序号 | 分组 | 组中值 | 频数 | 频率 |
1 | [60,70) | 65 | ① | 0.10 |
2 | [70,80) | 75 | 20 | ② |
3 | [80,90) | 85 | ③ | 0.20 |
4 | [90,100) | 95 | ④ | ⑤ |
合计 | 50 | 1 | ||
(1)求出频率分布表中①、②、③、④、⑤的值;
(2)为鼓励更多的学生了解“安全自救”知识,成绩不低于85分的学生能获奖,请估计在参加的800名学生中大约有多少名学生获奖?
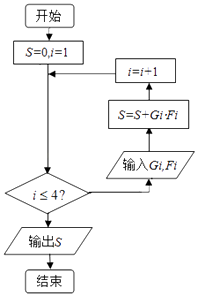
(3)在上述统计数据的分析中,有一项指标计算的程序框图如图所示,则该程序的功能是什么?求输出的S的值.
【题目】拖延症总是表现在各种小事上,但日积月累,特别影响个人发展.某校的一个社会实践调查小组,在对该校学生进行“是否有明显拖延症”的调查中,随机发放了110份问卷.对收回的100份有效问卷进行统计,得到如下![]() 列联表:
列联表:
有明显拖延症 | 无明显拖延症 | 合计 | |
男 | 35 | 25 | 60 |
女 | 30 | 10 | 40 |
合计 | 65 | 35 | 100 |
(Ⅰ)按女生是否有明显拖延症进行分层,已经从40份女生问卷中抽取了8份问卷,现从这8份问卷中再随机抽取3份,并记其中无明显拖延症的问卷的份数为![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若在犯错误的概率不超过![]() 的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的
的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |

