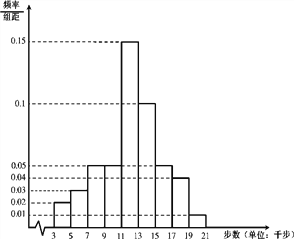
题目内容
【题目】为选拔选手参加“中国诗词大会”,某中学举行一次“诗词大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() ,
, ![]() 的数据).
的数据).
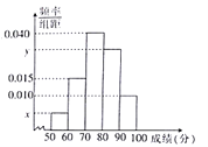
(1)求样本容量![]() 和频率分布直方图中
和频率分布直方图中![]() 、
、![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“中国谜语大会”,设随机变量![]() 表示所抽取的2名学生中得分在
表示所抽取的2名学生中得分在![]() 内的学生人数,求随机变量
内的学生人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.

【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)由频率分布直方图及题意可得样本容量![]() 与
与![]() 、
、![]() 的值;(2)抽取的2名学生中得分在
的值;(2)抽取的2名学生中得分在![]() 的人数X可能取值0,1,2,求出相应的概率值,即可得到随机变量
的人数X可能取值0,1,2,求出相应的概率值,即可得到随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
试题解析:
(1)由题意可知,样本容量![]() ,
,
![]() ;
;
(2)分数在![]() 内的学生有
内的学生有![]() 人, 分数在
人, 分数在![]() 内的学生有
内的学生有![]() 人,
人,
抽取的2名学生中得分在![]() 的人数X可能取值0,1,2,
的人数X可能取值0,1,2,
则![]() ,
, ![]() ,
, ![]() ,
,
则![]() 的分布列为
的分布列为

所以![]() .
.

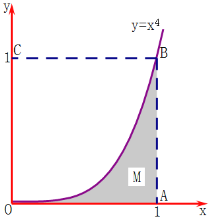
【题目】Monte-Carlo方法在解决数学问题中有广泛的应用.下面利用Monte-Carlo方法来估算定积分![]() .考虑到
.考虑到![]() 等于由曲线
等于由曲线![]() ,
,![]() 轴,直线
轴,直线![]() 所围成的区域
所围成的区域![]() 的面积,如图,在
的面积,如图,在![]() 外作一个边长为1正方形OABC.在正方形OABC内随机投掷n个点,若n个点中有m个点落入M中,则M的面积的估计值为
外作一个边长为1正方形OABC.在正方形OABC内随机投掷n个点,若n个点中有m个点落入M中,则M的面积的估计值为![]() ,此即为定积分
,此即为定积分![]() 的估计值.现向正方形OABC中随机投掷10000个点,以X表示落入M中的点的数目.
的估计值.现向正方形OABC中随机投掷10000个点,以X表示落入M中的点的数目.
(1)求X的期望![]() 和方差
和方差![]() ;
;
(2)求用以上方法估算定积分![]() 时,
时,![]() 的估计值与实际值之差在区间(-0.01,0.01)的概率.
的估计值与实际值之差在区间(-0.01,0.01)的概率.
附表:![]()
| 1899 | 1900 | 1901 | 2099 | 2100 | 2101 |
| 0.0058 | 0.0062 | 0.0067 | 0.9933 | 0.9938 | 0.9942 |