题目内容
【题目】已知![]() 为椭圆
为椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为其右焦点,
为其右焦点, ![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的动点,且
的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆在点
与椭圆在点![]() 处的切线交于点
处的切线交于点![]() ,当点
,当点![]() 在椭圆上运动时,求证:以
在椭圆上运动时,求证:以 ![]() 为直径的圆与直线
为直径的圆与直线![]() 恒相切.
恒相切.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析: (1)由题意知知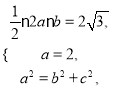 ,由此能求出椭圆
,由此能求出椭圆![]() 的方程;
的方程;
(2)设直线![]() 的方程为
的方程为![]() ,
, 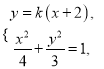 得
得![]() .,由此利用韦达定理、点到直线距离公式、直线与圆相切等知识点结合已知条件能证明当点
.,由此利用韦达定理、点到直线距离公式、直线与圆相切等知识点结合已知条件能证明当点![]() 在椭圆上运动时,以
在椭圆上运动时,以 ![]() 为直径的圆与直线
为直径的圆与直线![]() 恒相切.
恒相切.
试题解析:(1)设椭圆![]() 的方程为
的方程为![]() ,
,
由题意知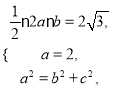 解之得
解之得![]() ,
,
故椭圆![]() 的方程为
的方程为![]() .
.
(2)证明:设直线![]() 的方程为
的方程为![]() .
.
则点![]() 坐标为
坐标为![]() 中点
中点![]() 的坐标为
的坐标为![]() .
.
由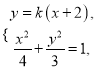 得
得![]() .
.
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() .
.
![]() .
.
![]() 点
点![]() 坐标为
坐标为![]() ,
,
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 轴,点
轴,点![]() 的坐标为
的坐标为![]() .
.
此时以![]() 为直径的圆
为直径的圆![]() 与直线
与直线![]() 相切.
相切.
当![]() 时,则直线
时,则直线![]() 的斜率
的斜率![]() .
.
![]() 直线
直线![]() 的方程为
的方程为![]() .
.
点E到直线![]() 的距离
的距离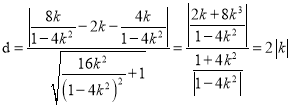 .
.
又因为![]() .
.
故以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
综上得,当点![]() 在椭圆上运动时,以
在椭圆上运动时,以![]() 为直径的圆与直径
为直径的圆与直径![]() 恒相切.
恒相切.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验.测得的数据如下:
零件数x(个) | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
加工时间y(分) | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(1)y与x是否具有线性相关关系?
(2)如果y与x具有线性相关关系,求回归直线方程;
(3)根据求出的回归直线方程,预测加工200个零件所用的时间为多少?
附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为![]() =
= ,
,![]() =
=![]() -
-![]() .
.