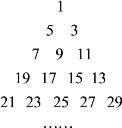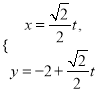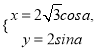题目内容
【题目】判断下列函数的奇偶性:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() ;
;
(5)![]() ;
;
(6)![]() ;
;
(7)![]() ;
;
(8)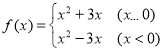
【答案】(1)非奇非偶;(2)既奇又偶;(3)非奇非偶;(4)非奇非偶;(5)偶;(6)奇;(7)奇;(8)偶
【解析】
先求函数的定义域,若定义域不关于原点对称,则该函数是非奇非偶函数;若定义域关于原点对称,且![]() ,则该函数是既奇又偶函数;若定义域关于原点对称,再计算
,则该函数是既奇又偶函数;若定义域关于原点对称,再计算![]() ,看
,看![]() 与
与![]() 、
、![]() 是否相等,然后按照奇偶函数定义判断;确定函数的定义域,有时能化简函数的解析式,以便简化解题过程,如(4)和(7)题;分段函数要分段分别判断;根据以上逐一判断即可.
是否相等,然后按照奇偶函数定义判断;确定函数的定义域,有时能化简函数的解析式,以便简化解题过程,如(4)和(7)题;分段函数要分段分别判断;根据以上逐一判断即可.
解:(1)![]() ,其定义域不关于原点对称,所以该函数是非奇非偶函数;
,其定义域不关于原点对称,所以该函数是非奇非偶函数;
(2)根据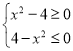 ,所以
,所以![]() 关于原点对称,又
关于原点对称,又![]()
![]() 是既奇又偶函数;
是既奇又偶函数;
(3)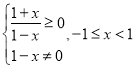 ,其定义域
,其定义域![]() 不关于原点对称,
不关于原点对称,
所以该函数是非奇非偶函数;
(4)![]() 的定义域是
的定义域是![]() 不关于原点对称,
不关于原点对称,
所以该函数是非奇非偶函数;
(5)![]() 的定义域是
的定义域是![]() 关于原点对称,
关于原点对称,
![]() ,所以该函数是偶函数;
,所以该函数是偶函数;
(6)![]() 的定义域是
的定义域是![]() 关于原点对称
关于原点对称
![]() ,所以该函数是奇函数;
,所以该函数是奇函数;
(7)![]() 定义域关于原点对称,此时
定义域关于原点对称,此时![]() ,
,
![]() ,所以该函数是奇函数;
,所以该函数是奇函数;
(8)函数定义域是![]() 关于原点对称,
关于原点对称,
当![]() ,则
,则![]() ,
,![]()
当![]() ,则
,则![]() ,
,![]()
![]() ,
,
所以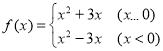 是偶函数
是偶函数

练习册系列答案
相关题目