题目内容
【题目】交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围为[0,10],分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如右图. (Ⅰ)这50个路段为中度拥堵的有多少个?
(Ⅱ)据此估计,早高峰三环以内的三个路段至少有一个是严重拥堵的概率是多少?
(III)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为36分钟;中度拥堵为42分钟;严重拥堵为60分钟,求此人所用时间的数学期望.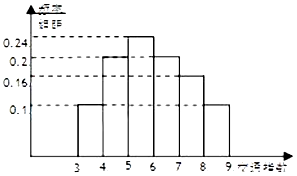
【答案】解:(Ⅰ)(0.2+0.16)×1×50=18,这50路段为中度拥堵的有18个. (Ⅱ)设事件A“一个路段严重拥堵”,则P(A)=0.1,
事件B 至少一个路段严重拥堵”,则P ![]() =(1﹣P(A))3=0.729.
=(1﹣P(A))3=0.729.
P(B)=1﹣P( ![]() )=0.271,所以三个路段至少有一个是严重拥堵的概率是0.271.
)=0.271,所以三个路段至少有一个是严重拥堵的概率是0.271.
(III)由频率分布直方图可得:分布列如下表:
X | 30 | 36 | 42 | 60 |
P | 0.1 | 0.44 | 0.36 | 0.1 |
E(X)=30×0.1+36×0.44+42×0.36+60×0.1=39.96.
此人经过该路段所用时间的数学期望是39.96分钟.
【解析】(Ⅰ)利用(0.2+0.16)×1×50即可得出这50路段为中度拥堵的个数.(Ⅱ)设事件A“一个路段严重拥堵”,则P(A)=0.1,事件B 至少一个路段严重拥堵”,则P ![]() =(1﹣P(A))3 . P(B)=1﹣P(
=(1﹣P(A))3 . P(B)=1﹣P( ![]() )=0.271,可得三个路段至少有一个是严重拥堵的概率.(III)利用频率分布直方图即可得出分布列,进而得出数学期望.
)=0.271,可得三个路段至少有一个是严重拥堵的概率.(III)利用频率分布直方图即可得出分布列,进而得出数学期望.
【考点精析】根据题目的已知条件,利用频率分布直方图的相关知识可以得到问题的答案,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
