题目内容
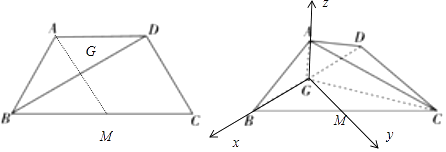
【题目】如图所示,在等腰梯形ABCD中,AD∥BC,AD=CD=AB,∠ABC=60°,将三角形ABD沿BD折起,使点A在平面BCD上的投影G落在BD上. 
(1)求证:平面ACD⊥平面ABD;
(2)求二面角G﹣AC﹣D的平面角的余弦值.
【答案】
(1)解:在等腰梯形ABCD中,∵AD∥BC,AD=CD=AB,∠ABC=60°,∴∠BAD=120°,从而∠ABD=∠ADB=30°,可得∠BDC=90°,
在三棱锥A﹣BCD中,∵点A在平面BCD上的投影G落在BD上,∴AG⊥BD,于是G为BD中点.
∵  ∴CD⊥面ABD,又CD面ADC,∴平面ACD⊥平面ABD
∴CD⊥面ABD,又CD面ADC,∴平面ACD⊥平面ABD
(2)解:由(1)得AG⊥面BCD,且G为BD中点,CD⊥面ABD,
取BC中点M,则MG∥CD,于是以G为原点,建立如图的空间直角坐标系G﹣xyz,
设AB=1,则BD= ![]() ,BC=2,CD=1,于是A(0,0,
,BC=2,CD=1,于是A(0,0, ![]() ),B(
),B( ![]() ,0,0).,C(﹣
,0,0).,C(﹣ ![]() ,1,0),D(﹣
,1,0),D(﹣ ![]() ,0,0)
,0,0)
![]() ,
, ![]() .
.
设面AGC的法向量为 ![]() ,由
,由  ,取
,取 ![]() ,
,
设面ADC的法向量为 ![]() ,由
,由 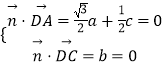 ,取
,取 ![]()
cos< ![]() ,
, ![]() >=
>= ![]() .
.
二面角G﹣AC﹣D的平面角的余弦值为 ![]()
【解析】(1)在等腰梯形ABCD中,可得∠ABD=∠ADB=30°,∠BDC=90°,在三棱锥A﹣BCD中,由点A在平面BCD上的投影G落在BD上,得CD⊥面ABD,又CD面ADC,即平面ACD⊥平面ABD;(2)取BC中点M,则MG∥CD,于是以G为原点,建立如图的空间直角坐标系G﹣xyz,设AB=1,则BD= ![]() ,BC=2,CD=1,于是A(0,0,
,BC=2,CD=1,于是A(0,0, ![]() ),B(
),B( ![]() ,0,0),C(﹣
,0,0),C(﹣ ![]() ,1,0),D(﹣
,1,0),D(﹣ ![]() ,0,0),利用法向量求解.
,0,0),利用法向量求解.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
,![]()