题目内容
【题目】设椭圆C: ![]() +
+ ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 点A({2,
=1(a>b>0)的左、右焦点分别为F1 , F2 , 点A({2, ![]() )在椭圆上,且满足
)在椭圆上,且满足 ![]()
![]() =0. (Ⅰ)求椭圆C的标准方程;
=0. (Ⅰ)求椭圆C的标准方程;
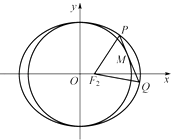
(Ⅱ)动直线l:y=kx+m与椭圆C交于P,Q两点,且OP⊥OQ,是否存在圆x2+y2=r2使得l恰好是该圆的切线,若存在,求出r;若不存在,说明理由.
【答案】解:(Ⅰ)∵ ![]() , ∴AF2⊥F1F2 ,
, ∴AF2⊥F1F2 ,
∵A在椭圆上,
∴ ![]() ,解得
,解得 ![]() .
.
∴ 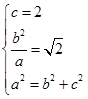 ,解得a2=8,b2=4,.
,解得a2=8,b2=4,.
∴椭圆 ![]() .
.
(Ⅱ)设P(x1 , y1),Q(x2 , y2),
将l:y=kx+m代入 ![]() ,整理得:(1+2k2)x2+4kmx+2m2﹣8=0,
,整理得:(1+2k2)x2+4kmx+2m2﹣8=0,
∵△>0,
∴8k2﹣m2+4>0,
且 ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∵OP⊥OQ,
∴x1x2+y1y2=0,即 ![]() ,
,
∴ ![]() ,
,
由 ![]() 和8k2﹣m+4>0,得
和8k2﹣m+4>0,得 ![]() 即可.
即可.
∵l与圆x2+y2=r2相切,
∴ ![]() ,
,
存在圆 ![]() 符合题意.
符合题意.
【解析】(1)由题意可知c=2,将A代入椭圆,列方程组,即可求得a和b的值,求得椭圆方程;(2)将直线l的方程代入椭圆方程,△>0,根据韦达定理定理求得x1+x2及x1x2 , 代入直线l方程求得y1y2 , 由OP⊥OQ,根据向量数量积的坐标表示求得x1x2+y1y2=0,求得m的取值范围,l与圆x2+y2=r2相切,代入即可求得r的值.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案【题目】某研究小组欲研究昼夜温差大小与患感冒人数之间的关系,统计得到1至6月份每月9号的昼夜温差![]() 与因患感冒而就诊的人数
与因患感冒而就诊的人数![]() 的数据,如下表:
的数据,如下表:
日期 | 1月9号 | 2月9号 | 3月9号 | 4月9号 | 5月9号 | 6月9号 |
| 10 | 11 | 13 | 12 | 8 | 6 |
| 22 | 25 | 29 | 26 | 16 | 12 |
该研究小组的研究方案是:先从这6组数据中选取2组,用剩下的4组数据求回归方程,再用之前被选取的2组数据进行检验.
(1)若选取1月和6月的数据作为检验数据,请根据剩下的2至5月的数据,求出![]() 关于
关于![]() 的线性回归方程;(计算结果保留最简分数)
的线性回归方程;(计算结果保留最简分数)
(2)若用(1)中所求的回归方程作预报,得到的估计数据与所选出的检验数据的误差不超过2人,则认为得到的回归方程是理想的,试问该研究小组所得回归方程是否理想?
【题目】(本题满分12分)全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.
组号 | 分组 | 频数 |
1 |
| 2 |
2 |
| 8 |
3 |
| 7 |
4 |
| 3 |
(Ⅰ)现从融合指数在![]() 和
和![]() 内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在
内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在![]() 的概率;
的概率;
(Ⅱ)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.