题目内容
【题目】如图,在四边形ABCD中,| ![]() |=4,
|=4, ![]() =12,E为AC的中点.
=12,E为AC的中点. 
(1)若cos∠ABC= ![]() ,求△ABC的面积S△ABC;
,求△ABC的面积S△ABC;
(2)若 ![]() =2
=2 ![]() ,求
,求 ![]()
![]() 的值.
的值.
【答案】
(1)解:∵ ![]() ,∠ABC∈(0,π);
,∠ABC∈(0,π);
∴ ![]() ;
;
∵ ![]() =
= ![]() ;
;
∴ ![]() ;
;
∴ ![]() =
= ![]()
(2)解:以E为原点,AC所在直线为x轴,建立如图所示平面直角坐标系:
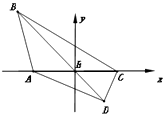
则A(﹣2,0),C(2,0),设D(x,y);
由 ![]() ,可得B(﹣2x,﹣2y);
,可得B(﹣2x,﹣2y);
则 ![]() =12;
=12;
∴x2+y2=4;
∴ ![]()
【解析】(1)容易求出sin∠ABC= ![]() ,并且可求出
,并且可求出 ![]() 的值,根据三角形面积公式即可求出△ABC的面积;(2)可以E为坐标原点,AC所在直线为x轴建立平面直角坐标系,并可得到A(﹣2,0),C(2,0),并设D(x,y),根据条件可求得E点坐标,从而求出
的值,根据三角形面积公式即可求出△ABC的面积;(2)可以E为坐标原点,AC所在直线为x轴建立平面直角坐标系,并可得到A(﹣2,0),C(2,0),并设D(x,y),根据条件可求得E点坐标,从而求出 ![]() 的坐标,进行数量积的坐标运算即可求得x2+y2=4,这样便可求出
的坐标,进行数量积的坐标运算即可求得x2+y2=4,这样便可求出 ![]() 的值.
的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目