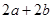题目内容
已知椭圆 +
+ =1,F1、F2分别为其左、右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长为( )
=1,F1、F2分别为其左、右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长为( )
 +
+ =1,F1、F2分别为其左、右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长为( )
=1,F1、F2分别为其左、右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长为( )| A.1 | B.2 | C.3 | D.4 |
D
试题分析:由椭圆定义知点M到两焦点的距离为
 ,因为M到F1的距离是2,所以
,因为M到F1的距离是2,所以 ,因为N是MF1的中点,
,因为N是MF1的中点,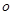 是
是 的中点,所以
的中点,所以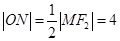 ,故D正确。
,故D正确。
练习册系列答案
相关题目
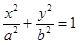 (a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,斜率为1的直线
(a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,斜率为1的直线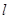 与椭圆C交于不同两点M,N.
与椭圆C交于不同两点M,N.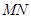 的长;
的长;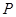 为椭圆
为椭圆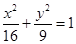 上的一点,
上的一点,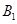 ,
,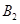 分别为椭圆的上、下顶点,若△
分别为椭圆的上、下顶点,若△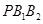 的面积为6,则满足条件的点
的面积为6,则满足条件的点 的一条渐近线方程为
的一条渐近线方程为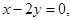 则椭圆
则椭圆 的离心率
的离心率
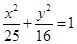 上的一点
上的一点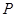 到椭圆一个焦点的距离为
到椭圆一个焦点的距离为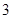 ,则
,则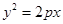 与椭圆
与椭圆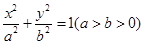 有相同的焦点
有相同的焦点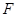 ,
,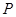 是两曲线的公共点,若
是两曲线的公共点,若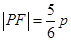 ,则此椭圆的离心率为 .
,则此椭圆的离心率为 .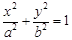 (a>b>0)的左、右焦点,过F1的直线
(a>b>0)的左、右焦点,过F1的直线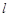 与
与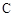 交于A,B两点.若AB⊥AF2,|AB|:|AF2|=3:4,则椭圆的离心率为 .
交于A,B两点.若AB⊥AF2,|AB|:|AF2|=3:4,则椭圆的离心率为 .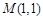 作一直线与椭圆
作一直线与椭圆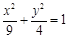 相交于A、B两点,若
相交于A、B两点,若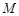 点恰好为弦
点恰好为弦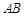 的中点,则
的中点,则 是椭圆
是椭圆 的两个焦点,
的两个焦点, 是过
是过 的弦,则
的弦,则 的周长是( )
的周长是( )