题目内容
设F1,F2是椭圆C: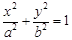 (a>b>0)的左、右焦点,过F1的直线
(a>b>0)的左、右焦点,过F1的直线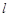 与
与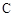 交于A,B两点.若AB⊥AF2,|AB|:|AF2|=3:4,则椭圆的离心率为 .
交于A,B两点.若AB⊥AF2,|AB|:|AF2|=3:4,则椭圆的离心率为 .
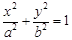 (a>b>0)的左、右焦点,过F1的直线
(a>b>0)的左、右焦点,过F1的直线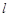 与
与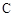 交于A,B两点.若AB⊥AF2,|AB|:|AF2|=3:4,则椭圆的离心率为 .
交于A,B两点.若AB⊥AF2,|AB|:|AF2|=3:4,则椭圆的离心率为 . .
.试题分析:设
 ,因AB⊥AF2,则
,因AB⊥AF2,则 ,由椭圆的定义得
,由椭圆的定义得 ,所以
,所以 ,
, ,则椭圆的离心率为
,则椭圆的离心率为 .
.
练习册系列答案
相关题目
题目内容
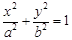 (a>b>0)的左、右焦点,过F1的直线
(a>b>0)的左、右焦点,过F1的直线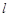 与
与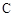 交于A,B两点.若AB⊥AF2,|AB|:|AF2|=3:4,则椭圆的离心率为 .
交于A,B两点.若AB⊥AF2,|AB|:|AF2|=3:4,则椭圆的离心率为 . .
. ,因AB⊥AF2,则
,因AB⊥AF2,则 ,由椭圆的定义得
,由椭圆的定义得 ,所以
,所以 ,
, ,则椭圆的离心率为
,则椭圆的离心率为 .
.