题目内容
如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,
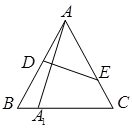
(1)①设A1B=x,用x表示AD;②设∠A1AB=θ∈[0º,60º],用θ表示AD
(2)求AD长度的最小值.
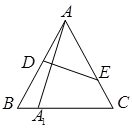
(1)①设A1B=x,用x表示AD;②设∠A1AB=θ∈[0º,60º],用θ表示AD
(2)求AD长度的最小值.
(1) y=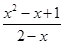 (0≤x≤1), AD=
(0≤x≤1), AD=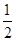 ·
·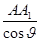 =
=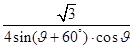 θ∈[0º,60º]
θ∈[0º,60º]
(2) AD长度的最小值为2 -3 当且仅当
-3 当且仅当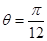 时取得最小值.
时取得最小值.
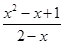 (0≤x≤1), AD=
(0≤x≤1), AD=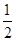 ·
·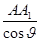 =
=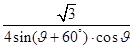 θ∈[0º,60º]
θ∈[0º,60º](2) AD长度的最小值为2
 -3 当且仅当
-3 当且仅当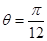 时取得最小值.
时取得最小值.试题分析:(1)设A1B=x,AD=y,在△A1BD中,BD=1-y,A1D=AD=y,有余弦定理得
y2=(1-y)2+x2-2x(1-y)cos60º=(1-y)2+x2-x+xy∴x2-x+xy-2y+1=0
y=
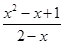 (0≤x≤1),
(0≤x≤1), 设∠A1AB=θ∈[0º,60º],则在△A1BA中,由正弦定理得:
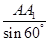 =
=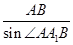 =
=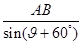 ∴AA1=
∴AA1=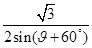 ,
,∴AD=
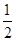 ·
·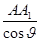 =
=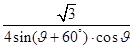 θ∈[0º,60º]
θ∈[0º,60º](2)y=
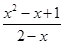 (0≤x≤1),令t=2-x∈[1,2]∴y=
(0≤x≤1),令t=2-x∈[1,2]∴y=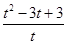 =t+
=t+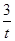 -3≥2
-3≥2 -3
-3当且仅当t=
 ,即x=2-
,即x=2- 时等号成立.AD长度的最小值为2
时等号成立.AD长度的最小值为2 -3.
-3.AD=
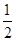 ·
·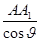 =
=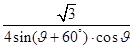 θ∈[0º,60º]
θ∈[0º,60º]∵4sin(θ+60º)·cosθ=2sinθ·cosθ+2
 cos2θ=sin2θ+
cos2θ=sin2θ+ (1+cos2θ)=sin2θ+
(1+cos2θ)=sin2θ+ cos2θ+
cos2θ+ =2sin(2θ+60º)+
=2sin(2θ+60º)+
∵θ∈[0º,60º]∴2θ+60º∈[60º,180º]∴sin(2θ+60º)∈[0,1]
∴4sin(θ+60º)·cosθ∈[
 ,2+
,2+ ]∴AD≥
]∴AD≥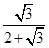 =
= (2-
(2- )=2
)=2 -3∴AD长度的最小值为2
-3∴AD长度的最小值为2 -3 当且仅当
-3 当且仅当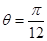 时取得最小值.
时取得最小值.点评:本小题主要考查正弦定理、余弦定理等基础知识,同时考查利用三角公式进行恒等变形的技能和运算能力

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
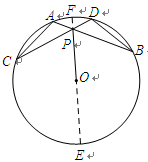
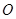 的半径为3,两条弦
的半径为3,两条弦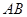 ,
,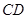 交于点
交于点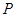 ,且
,且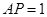 ,
, 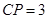 ,
,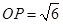 .
.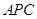 ≌△
≌△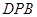 .
.
 ,则
,则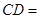
 为锐角△
为锐角△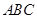 的内心,且
的内心,且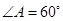 ,点
,点 为内切圆
为内切圆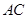 的切点,过点
的切点,过点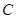 作直线
作直线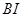 的垂线,垂足为
的垂线,垂足为 .
.
 ;
; 的值.
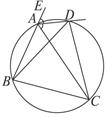
的值.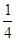 圆周,C点是弧BE上的任意一点, △ABD是等边三角形,则四边形ABCD的周长p的取值范围是
圆周,C点是弧BE上的任意一点, △ABD是等边三角形,则四边形ABCD的周长p的取值范围是 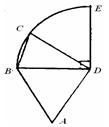
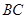 是半径为
是半径为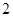 的圆
的圆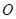 的直径,点
的直径,点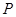 在
在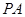 是圆
是圆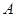 在直径
在直径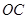 的中点,则
的中点,则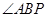 =
= 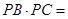 .
.
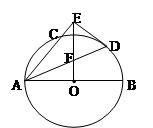
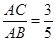 ,求
,求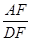 的值.
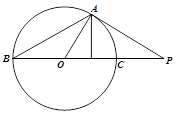
的值.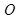 的切线,A为切点,割线PBC过圆心O,PA=10,PB=5,则AC长为
的切线,A为切点,割线PBC过圆心O,PA=10,PB=5,则AC长为 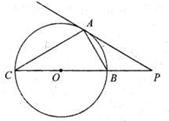
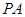 是圆
是圆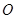 的切线,切点为
的切线,切点为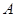 ,直线
,直线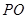 交圆
交圆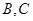 两点,
两点,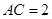 ,
, ,则圆
,则圆