题目内容
1.下面各命题中,正确的是( )| A. | 过平面外一点作与这个平面垂直的平面有且只有一个 | |
| B. | 若两条直线与一个平面所成的角相等,则这两条直线平行 | |
| C. | 若一个平面内有无数条直线与另一个平面平行,则这两个平面平行 | |
| D. | 若两个平面平行,则其中一个平面内的所有直线都与另一个平面平行 |
分析 A,B,C列举所有情况,D考虑线面平行的性质定理及平行公理即可.
解答 解:A、过平面外一点作与这个平面垂直的平面有无数个,故A错误;
B、若两条直线和同一个平面所成的角相等,则这两条直线平行、相交或异面,故A错误;
C、若一个平面内有无数条直线与另一个平面平行,则这两个平面可能相交或平行,故C错误;
D、若两个平面平行,则其中一个平面内的所有直线都与另一个平面平行,故D正确;
故选:D.
点评 本题主要考查了空间线面、面面位置关系,要求熟练掌握相应的定义和定理,注意定理成立的条件.

练习册系列答案
相关题目
12.复数$1+\frac{5}{2-i}$(i是虚数单位)的模等于( )
| A. | $\sqrt{10}$ | B. | 10 | C. | $\sqrt{5}$ | D. | 5 |
9.在花园小区内有一块三边长分别为6米、8米、10米的三角形绿化地,有一只小狗在其内部玩耍,若不考虑小狗的大小,则在任意指定的某时刻,小狗与三角形三个顶点的距离均超过2米的概率是( )
| A. | 1-$\frac{π}{24}$ | B. | 1$-\frac{π}{6}$ | C. | 1$-\frac{π}{12}$ | D. | 2$-\frac{π}{3}$ |
6.已知函数f(x)=cos(2x+φ)(φ为常数)为奇函数,那么cosφ=( )
| A. | -$\frac{{\sqrt{2}}}{2}$ | B. | 0 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 1 |
13.圆C:x2+y2+4x-2y+3=0的圆心坐标及半径分别是( )
| A. | (-2,1),$\sqrt{2}$ | B. | (2,1),$\sqrt{2}$ | C. | (-2,1),2 | D. | (2,-1),2 |
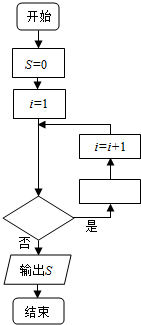 如图是计算1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2015}$的值的程序框图.
如图是计算1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2015}$的值的程序框图. 已知函数$y=sin(ωx+φ)(ω>0,0<φ≤\frac{π}{2})$的部分图象如图所示.
已知函数$y=sin(ωx+φ)(ω>0,0<φ≤\frac{π}{2})$的部分图象如图所示.