题目内容
9.在花园小区内有一块三边长分别为6米、8米、10米的三角形绿化地,有一只小狗在其内部玩耍,若不考虑小狗的大小,则在任意指定的某时刻,小狗与三角形三个顶点的距离均超过2米的概率是( )| A. | 1-$\frac{π}{24}$ | B. | 1$-\frac{π}{6}$ | C. | 1$-\frac{π}{12}$ | D. | 2$-\frac{π}{3}$ |
分析 根据题意,记“小狗距三角形三个顶点的距离均超过2”为事件A,则其对立事件$\overline{A}$为“小狗与三角形的三个顶点的距离不超过2”,先求得边长为4的等边三角形的面积,再计算事件构成的区域面积,由几何概型可得P($\overline{A}$),进而由对立事件的概率性质,可得答案
解答 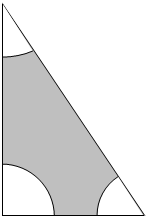 解:记“小狗距三角形三个顶点的距离均超过2米”为事件A,则其对立事件$\overline{A}$为“小狗与三角形的三个顶点的距离不超过2米”,如图阴影部分,
解:记“小狗距三角形三个顶点的距离均超过2米”为事件A,则其对立事件$\overline{A}$为“小狗与三角形的三个顶点的距离不超过2米”,如图阴影部分,
三边长分别为6米、8米、10米的三角形的面积为S=$\frac{1}{2}×6×8$=24,
则事件$\overline{A}$构成的区域为分别以三角形的三个顶点为圆心半径为2的扇形,恰好可组合成一个半圆,其面积为S($\overline{A}$)=$\frac{1}{2}×π×{2}^{2}$=2π,
由几何概型的概率公式得P($\overline{A}$)=$\frac{2π}{24}=\frac{π}{12}$;
P(A)=1-P($\overline{A}$)=1-$\frac{π}{12}$.
故选:C.
点评 本题主要考查几何概型,涉及对立事件的概率性质,解题时如需要计算不规则图形的面积,可用间接法.同时考查了分析问题的能力,属于中档题.

练习册系列答案
相关题目
17.函数f(x)=sin$\frac{2}{3}x+cos\frac{2}{3}$x的图象中相邻的两条对称轴间距离为( )
| A. | $\frac{3}{2}π$ | B. | $\frac{4}{3}π$ | C. | 3π | D. | $\frac{7}{6}π$ |
4.在投掷一枚硬币的试验中,共投掷了100次,“正面朝上”的频数49,则“正面朝上”的频率为( )
| A. | 0.49 | B. | 0.5 | C. | 0.51 | D. | 49 |
1.下面各命题中,正确的是( )
| A. | 过平面外一点作与这个平面垂直的平面有且只有一个 | |
| B. | 若两条直线与一个平面所成的角相等,则这两条直线平行 | |
| C. | 若一个平面内有无数条直线与另一个平面平行,则这两个平面平行 | |
| D. | 若两个平面平行,则其中一个平面内的所有直线都与另一个平面平行 |
18.已知不等式组$\left\{\begin{array}{l}x+y≥4\\ x-y≥-2\\ x≤2\end{array}\right.$表示的平面区域为D,点O(0,0),A(1,0).若点M是D上的动点,则$\frac{{\overrightarrow{OA}•\overrightarrow{OM}}}{{|{\overrightarrow{OM}}|}}$的最小值是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
19.已知f(x)=x3-6x2+9x+2,f′(x)是f(x)的导数,f(x)和f′(x)单调性相同的区间是( )
| A. | [1,2]∪[3,+∞) | B. | [1,2]和[3,+∞) | C. | (-∞,2] | D. | [2,+∞) |