题目内容
13.圆C:x2+y2+4x-2y+3=0的圆心坐标及半径分别是( )| A. | (-2,1),$\sqrt{2}$ | B. | (2,1),$\sqrt{2}$ | C. | (-2,1),2 | D. | (2,-1),2 |
分析 把圆的一般方程化为标准方程,即可得到圆心坐标及半径.
解答 解:圆C:x2+y2+4x-2y+3=0,即 圆C:(x+2)2+(y-1)2 =2,
故圆心为(-2,1)、半径为$\sqrt{2}$,
故选:A.
点评 本题主要考查圆的一般方程,属于基础题.

练习册系列答案
相关题目
4.在投掷一枚硬币的试验中,共投掷了100次,“正面朝上”的频数49,则“正面朝上”的频率为( )
| A. | 0.49 | B. | 0.5 | C. | 0.51 | D. | 49 |
1.下面各命题中,正确的是( )
| A. | 过平面外一点作与这个平面垂直的平面有且只有一个 | |
| B. | 若两条直线与一个平面所成的角相等,则这两条直线平行 | |
| C. | 若一个平面内有无数条直线与另一个平面平行,则这两个平面平行 | |
| D. | 若两个平面平行,则其中一个平面内的所有直线都与另一个平面平行 |
18.已知不等式组$\left\{\begin{array}{l}x+y≥4\\ x-y≥-2\\ x≤2\end{array}\right.$表示的平面区域为D,点O(0,0),A(1,0).若点M是D上的动点,则$\frac{{\overrightarrow{OA}•\overrightarrow{OM}}}{{|{\overrightarrow{OM}}|}}$的最小值是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
5.sin$\frac{20π}{3}$的值为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
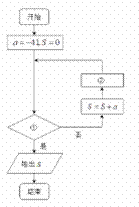 右图表示的是求首项为-41,公差为2的等差数列{an}前n项和的最小值的程序框图.①处可填写a>0;②处可填写a=a+2.
右图表示的是求首项为-41,公差为2的等差数列{an}前n项和的最小值的程序框图.①处可填写a>0;②处可填写a=a+2.