题目内容
16.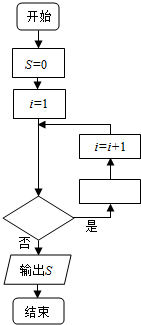 如图是计算1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2015}$的值的程序框图.
如图是计算1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2015}$的值的程序框图.(1)图中空白的判断框应填i≤2015或i<2016.执行框应填S=S+$\frac{1}{i}$.
(2)写出与程序框图相对应的程序.
分析 (1)分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S的值,分析可得解;
(2)根据框图和算法即可写出相应的程序.
解答 解:(1)程序运行过程中,各变量值如下表所示:
第一圈:S=0+1,i=2,
第二圈:S=1+$\frac{1}{2}$,i=3,
第三圈:S=1+$\frac{1}{2}+\frac{1}{3}$,i=4,
…
依此类推,第2015圈:S=1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2015}$,i=2016,退出循环,
其中应填入的条件是:判断框:i≤2015或i<2016,执行框:S=S+$\frac{1}{i}$,
故答案为:i≤2015或i<2016,S=S+$\frac{1}{i}$.
(2)程序如下:
S=0
i=1
WHILE i<=2015
S=S+1/i
i=i+1
WEND
PRINT S
END
点评 算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,本题属于基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
4.在投掷一枚硬币的试验中,共投掷了100次,“正面朝上”的频数49,则“正面朝上”的频率为( )
| A. | 0.49 | B. | 0.5 | C. | 0.51 | D. | 49 |
11.某校高一年段为了控制学生迟到现象,特别规定在每周周一到周五这五天中,“连续5天,每天迟到都不超过5人次的班级才有资格争夺年段流动红旗”.根据过去5天年段统计的一到四班迟到学生人此数据的数字特征,一定有资格的是( )
| A. | 一班:总体均值为2,总体方差为2 | B. | 二班:总体均值为3,中位数为3 | ||
| C. | 三班:总体均值为2,总体方差大于0 | D. | 四班:中位数为2,众数为2 |
1.下面各命题中,正确的是( )
| A. | 过平面外一点作与这个平面垂直的平面有且只有一个 | |
| B. | 若两条直线与一个平面所成的角相等,则这两条直线平行 | |
| C. | 若一个平面内有无数条直线与另一个平面平行,则这两个平面平行 | |
| D. | 若两个平面平行,则其中一个平面内的所有直线都与另一个平面平行 |
5.sin$\frac{20π}{3}$的值为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
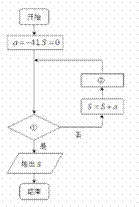 右图表示的是求首项为-41,公差为2的等差数列{an}前n项和的最小值的程序框图.①处可填写a>0;②处可填写a=a+2.
右图表示的是求首项为-41,公差为2的等差数列{an}前n项和的最小值的程序框图.①处可填写a>0;②处可填写a=a+2.