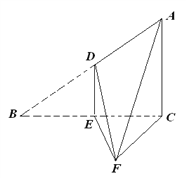
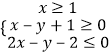题目内容
【题目】把一颗骰子投掷两次,记第一次出现的点数为a,第二次出现的点数为b.已知方程组 ![]() .
.
(1)求方程组只有一个解的概率;
(2)若方程组每个解对应平面直角坐标系中点P(x,y),求点P落在第四象限的概率.
【答案】
(1)解:把一颗骰子投掷两次,记第一次出现的点数为a,第二次出现的点数为b,
则基本事件空间Ω={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),
(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),
(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),
(5,2),(5,3),(5,4)(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),
(6,5),(6,6)}共有36种,
设方程组只有一个解为事件A,则事件A的对立事件是方程组无解,
若方程组无解,则两线平行, ![]() ,即a=2b,此时有3个满足,(2,1),(4,2),(6,3),
,即a=2b,此时有3个满足,(2,1),(4,2),(6,3),
所以,方程组只有一个解的概率 ![]() .
.
(2)解:设点P落在第四象限为事件B,
由方程组 ![]() ,得
,得 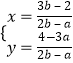 ,
,
若点P落在第四象限,则有 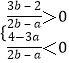 ,
,
当2b﹣a>0时, 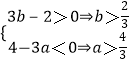 ,
,
即 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
所以符合条件的数组B={(2,2),(2,3),(3,2),(3,3),(3,4),(3,5),
(4,2),(4,3),(4,4),(4,5),(4,6)(5,2),(5,3),(5,4),(5,5),
(5,6)(6,2),(6,3),(6,4),(6,5),(6,6)}共21组.
当2b﹣a<0时, 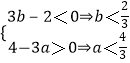 ,不存在符合条件的数组.
,不存在符合条件的数组.
所以,点P落在第四象限的概率 ![]() .
.
【解析】(1)利用列举法求出基本事件空间Ω,设方程组只有一个解为事件A,则事件A的对立事件是方程组无解,由此利用对立事件概率计算公式能求出方程组只有一个解的概率.(2)设点P落在第四象限为事件B,利用列举法求出符合条件的数组的个数,由此能求出点P落在第四象限的概率.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】已知函数![]() ),记
),记![]() 的导函数为
的导函数为![]() .
.
(1) 证明:当![]() 时,
时, ![]() 在
在![]() 上的单调函数;
上的单调函数;
(2)若![]() 在
在![]() 处取得极小值,求
处取得极小值,求![]() 的取值范围;
的取值范围;
(3)设函数![]() 的定义域为
的定义域为![]() ,区间
,区间![]() .若
.若![]() 在
在![]() 上是单调函数,则称
上是单调函数,则称![]() 在
在![]() 上广义单调.试证明函数
上广义单调.试证明函数![]() 在
在![]() 上广义单调.
上广义单调.
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问部分职工,根据被访问职工对该部门的评分,绘制频率分布直方图(如图所示).
(1)求频率分布表中①、②、③位置相应数据,并在答题纸上完成频率分布直方图;
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 5 | 0.050 |
第2组 | [60,70) | ① | 0.350 |
第3组 | [70,80) | 30 | ② |
第4组 | [80,90) | 20 | 0.200 |
第5组 | [90,100] | 10 | 0.100 |
合计 | ③ | 1.00 | |
(2)为进一步了解情况,该企业决定在第3,4,5组中用分层抽样抽取5名职工进行座谈,求第3,4,5组中各自抽取的人数;
(3)求该样本平均数 ![]() .
.