题目内容
【题目】已知函数![]() ),记
),记![]() 的导函数为
的导函数为![]() .
.
(1) 证明:当![]() 时,
时, ![]() 在
在![]() 上的单调函数;
上的单调函数;
(2)若![]() 在
在![]() 处取得极小值,求
处取得极小值,求![]() 的取值范围;
的取值范围;
(3)设函数![]() 的定义域为
的定义域为![]() ,区间
,区间![]() .若
.若![]() 在
在![]() 上是单调函数,则称
上是单调函数,则称![]() 在
在![]() 上广义单调.试证明函数
上广义单调.试证明函数![]() 在
在![]() 上广义单调.
上广义单调.
【答案】(1)![]() 在
在![]() 上单调递增.(2)
上单调递增.(2)![]() (3)见解析
(3)见解析
【解析】【试题分析】(1)借助题设条件运用导数与函数的单调性之间的关系判定;(2)依据题设条件运用极值的定义进行分析探求;(3)构造函数运用导数知识分析推证:
解:(1)当![]() 时,
时, ![]() ,即
,即![]() ,
, ![]() 在
在![]() 上单调递增.
上单调递增.
(2) ![]() . ①当
. ①当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增.若
上单调递增.若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ,所以函数
,所以函数![]() 的单调增区间是
的单调增区间是![]() ,单调减区间是
,单调减区间是![]() ,所以
,所以![]() 在
在![]() 处取得极小值,符合题意.②当
处取得极小值,符合题意.②当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减.若
上单调递减.若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ,所以
,所以![]() 的单调减区间是
的单调减区间是![]() ,单调增区间是
,单调增区间是![]() ,所以
,所以![]() 在
在![]() 处取得极大值,不符合题意. ③当
处取得极大值,不符合题意. ③当![]() 时,
时, ![]() ,使得
,使得![]() ,即
,即![]() ,但当
,但当![]() 时,
时, ![]() ,即
,即![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,即函数
,即函数![]() 在
在![]() 单调递减,不符合题意.综上所述,
单调递减,不符合题意.综上所述, ![]() 的取值范围是
的取值范围是![]() .
.
(3)记![]() . ①若
. ①若![]() ,注意到
,注意到![]() ,则
,则![]() ,即
,即![]() , 当
, 当 时,
时, ![]()
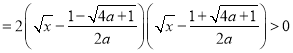 .
.
所以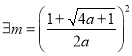 ,函数
,函数![]() 在
在![]() 上单调递增.②若
上单调递增.②若![]() ,当
,当![]() 时,
时, ![]() ,所以
,所以![]() ,函数
,函数![]() 在
在![]() 上单调递减,综上所述,函数
上单调递减,综上所述,函数![]() 在区间
在区间![]() 上广义单调.
上广义单调.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案【题目】已知某企业近3年的前7个月的月利润(单位:百万元)如下面的折线图所示:
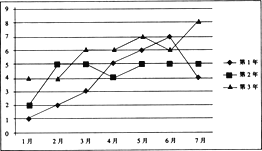
(1)试问这3年的前7个月中哪个月的月平均利润最高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
月份x | 1 | 2 | 3 | 4 |
利润y(单位:百万元) | 4 | 4 | 6 | 6 |
相关公式: 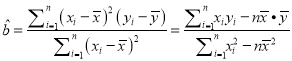 ,
, ![]() .
.
【题目】已知椭圆C1、抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点O,从每条曲线上取两个点,将其坐标记录于下表中:
x | 3 | ﹣2 | 4 |
|
y | ﹣2 | 0 | ﹣4 |
|
(1)求C1、C2的标准方程;
(2)请问是否存在直线l满足条件:①过C2的焦点F;②与C1交不同两点M、N且满足 ![]() ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.