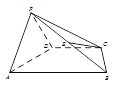题目内容
【题目】如图,直角![]() 中,∠
中,∠![]() ,
,![]() ,D、E分别是AB、BC边的中点,沿DE将
,D、E分别是AB、BC边的中点,沿DE将![]() 折起至
折起至![]() ,且∠
,且∠![]() .
.
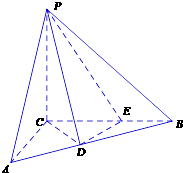
(Ⅰ)求四棱锥F-ADEC的体积;
(Ⅱ)求证:平面ADF⊥平面ACF.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(Ⅰ)可作![]() 于
于![]() ,利用所给条件,可证
,利用所给条件,可证![]() 为棱锥底面上的高且求出其长度,再进一步求出底面梯形的面积,可求得四棱锥体积;(Ⅱ)取线段AF、CF的点N、Q,进一步证明
为棱锥底面上的高且求出其长度,再进一步求出底面梯形的面积,可求得四棱锥体积;(Ⅱ)取线段AF、CF的点N、Q,进一步证明![]() ,可证得两平面垂直.
,可证得两平面垂直.
试题解析:(Ⅰ)D、E分别是AB、BC边的中点,![]() 平行且等于
平行且等于![]() 的一半,
的一半,![]() ,
,![]()
依题意,![]() ,
,![]() ,∵
,∵![]() ,
,![]() ,∵
,∵![]() ,
,![]()
作![]() 于
于![]() ,则
,则![]() ,∵∠
,∵∠![]() ,
,![]()
梯形![]() 的面积
的面积![]()
四棱锥F-ADEC的体积![]()
(Ⅱ)(法一)取线段AF、CF的点N、Q,连接DN、NQ、EQ,则NQ平行且等于![]() 的一半,
的一半,![]() NQ平行且等于DE,DEQN是平行四边形,DN//EQ
NQ平行且等于DE,DEQN是平行四边形,DN//EQ
∵EC=EF,∠![]() ,
,![]() 是等边三角形,EQ
是等边三角形,EQ![]() ,又∵
,又∵![]() ,
,![]() ,
,![]() AC
AC![]() ,∵
,∵![]() ,
,![]()
![]() ,又
,又![]() ,
,![]()
(法二)连接BF,∵EC=EF,∠![]() ,
,![]() 是边长为2等边三角形
是边长为2等边三角形
∵BE=EF,![]() ,
,![]() ,
,![]()
![]() ,DE//AC,
,DE//AC,![]()
∵![]() ,
,![]() ,又∵
,又∵![]() ,,
,,![]()
又∵![]() ,
,![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目