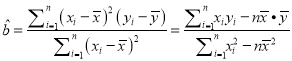题目内容
【题目】设f(n)是定义在N*上的增函数，f(4)＝5，且满足：
①任意n∈N*，f(n)
Z；②任意m，n∈N*，有f(m)f(n)＝f(mn)＋f(m＋n－1)．
（1）求f(1)，f(2)，f(3)的值；
（2）求f(n)的表达式．
【答案】（1）f(1)＝2，f(2)＝3，f(3)＝4；（2）f (n)＝n+1.
【解析】试题分析：（1）利用已知的表达式，通过
，直接求
，利用函数的单调性以及
，即可求出
的值；（2）利用函数的单调性及数学归纳法，推出
，又
，然后求出
的表达式 .
试题解析：（1）因为f(1)f(4)＝f(4)＋f(4)，所以5 f(1)＝10，则f(1)＝2．
因为f(n)是单调增函数
所以2＝f(1)＜f(2)＜f(3)＜f(4)＝5．
因为f(n)∈Z，所以f(2)＝3，f(3)＝4．
（2）解：由（1）可猜想f (n)＝n+1．
证明：因为f (n)单调递增，所以f (n+1)＞f (n)，又f(n)∈Z，
所以f (n+1)≥f (n)+1．
首先证明：f (n)≥n+1．
因为f (1)＝2，所以n＝1时，命题成立．
假设n=k(k≥1)时命题成立，即f(k)≥k+1．
则f(k+1)≥f (k)+1≥k+2，即n＝k+1时，命题也成立．
综上，f (n)≥n+1．
由已知可得f (2)f (n)＝f (2n)＋f (n+1)，而f(2)＝3，f (2n)≥2n＋1，
所以3 f (n)≥f (n+1)＋2n＋1，即f(n+1)≤3 f (n)－2n－1．
下面证明：f (n)＝n+1．
因为f (1)＝2，所以n＝1时，命题成立．
假设n=k(k≥1)时命题成立，即f(k)＝k+1，
则f(k+1)≤3f (k)－2k－1＝3(k+1)－2k－1＝k＋2，
又f(k+1)≥k＋2，所以f(k+1)＝k＋2．
即n＝k+1时，命题也成立．
所以f (n)＝n+1
