题目内容
【题目】已知数列
的前
项和为
，且满足
．
（1）求证：数列为等比数列；
（2）若
，求
的前
项和
．
【答案】（1）证明见解析；（2）
.
【解析】
试题分析：（1）利用
，化简得
，故
是等比数列；（2）由于
，相等于一个等差数列乘以一个等比数列，所以考虑用错位相减求和法求前
项和为
.
试题解析：
（1）当
时，
，解得
；．．．．．．．．．．．．．．．1分
当
时，
，两式相减得
，．．．．．．．．．．．．．．．．3分
化简得，所以数列
是首项为1，公比为-1的等比数列．．．．．．．．．．5分
（2）由（1）可得
，所以
，下提供三种求和方法供参考：．．．．．．．6分
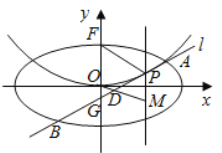
【错位相减法】
，
．．．．．．．．．．．．．．．．．．．．8分
两式相减得
．．．．．．．．．．．．．．．．9分
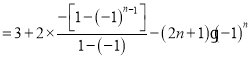．．．．．．．．．．．．．．．．．．．．10分
，．．．．．．．．．．．．．．．．．．．．11分
所以数列
的前
项和．．．．．．．．．．．．．．．．．．．．．．．．．12分
【并项求和法】/p>
当
为偶数时，
；．．．．．．．．．．．．．．．．．．．．．．．．9分
当
为奇数时，
为偶数，
；．．．．．．．．．．．．11分
综上，数列的前
项和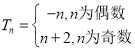
．．．．．．．．．．．．．．．．．．．．．．．．．12分
【裂项相消法】
因为
．．．．．．．．．．．．．．9分
所以
，
所以数列的前
项和
．．．．．．．．．．．．．．．．．．12分
激活思维优加课堂系列答案
活力试卷系列答案
【题目】某种产品的年销售量
与该年广告费用支出
有关，现收集了4组观测数据列于下表：
| 1 | 4 | 5 | 6 |
| 30 | 40 | 60 | 50 |
现确定以广告费用支出
为解释变量，销售量
为预报变量对这两个变量进行统计分析.
（1）已知这两个变量满足线性相关关系，试建立
与
之间的回归方程；
（2）假如2017年广告费用支出为10万元，请根据你得到的模型，预测该年的销售量
.
（线性回归方程系数公式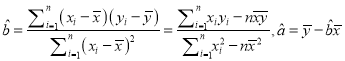
）.
