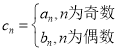题目内容
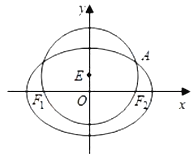
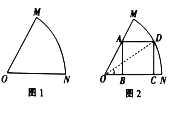
【题目】某车间为了制作某个零件,需从一块扇形的钢板余料(如图1)中按照图2的方式裁剪一块矩形钢板![]() ,其中顶点
,其中顶点![]() 、
、![]() 在半径
在半径![]() 上,顶点
上,顶点![]() 在半径
在半径![]() 上,顶点
上,顶点![]() 在
在![]() 上,
上, ![]() ,
, ![]() .设
.设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() .
.
(1)用含![]() 的式子表示
的式子表示![]() ,
, ![]() 的长;
的长;
(2)试将![]() 表示为
表示为![]() 的函数;
的函数;
(3)求![]() 的最大值.
的最大值.
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]()
![]() (
(![]() );(3)
);(3)![]() .
.
【解析】试题分析:(1)直角三角形中,根据锐角三角函数的定义即可表示出![]() 的值;(2 )求出
的值;(2 )求出![]() ,代入面积公式得出S关于
,代入面积公式得出S关于![]() 的函数;(3)利用二倍角公式及辅助角公式,三角恒等变换化简
的函数;(3)利用二倍角公式及辅助角公式,三角恒等变换化简![]() ,根据的
,根据的![]() 范围和正弦函数的性质即可得出S的最大值.
范围和正弦函数的性质即可得出S的最大值.
试题解析:(1)因为![]() ,四边形
,四边形![]() 是矩形,
是矩形,
所以在![]() 中,
中, ![]() .
.
所以![]() .
.
在![]() 中,
中, 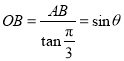 .
.
(2)在![]() 中,
中, ![]() .
.
所以![]() .
.
所以![]()
![]()
![]() (
(![]() ).
).
(3)因为![]()
![]() ,
,
![]()
![]() (
(![]() ),
),
所以,当![]() ,即
,即![]() 时,
时, ![]() 取得最大值
取得最大值![]() .
.
【方法点晴】本题考查的知识点比较多,主要考查等比数列的定义、余弦定理及三角函数的最值,属于难题.求与三角函数有关的最值常用方法有以下几种:①化成![]() 的形式利用配方法求最值;②形如
的形式利用配方法求最值;②形如![]() 的可化为
的可化为![]() 的形式利用三角函数有界性求最值;③
的形式利用三角函数有界性求最值;③![]() 型,可化为
型,可化为![]() 求最值 .本题(3)是利用方法③的思路解答的.
求最值 .本题(3)是利用方法③的思路解答的.

练习册系列答案
相关题目