题目内容
4.函数y=sinx在[-π,π]上的图象是( )| A. |  | B. |  | C. |  | D. | 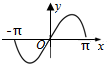 |
分析 由条件根据正弦函数的图象特征,可得结论.
解答 解:函数y=sinx在[-π,π]上是奇函数,它的图象关于原点对称,
故选:D.
点评 本题主要考查正弦函数的图象特征,属于基础题.

练习册系列答案
相关题目
12.已知幂函数f(x)=kxa(k∈R,a∈R)的图象经过点($\frac{1}{2},\frac{1}{4}$),则k+a=3;函数y=$\sqrt{3-2x-f(x)}$的定义域为[-3,1].
19.如图是函数f(x)=x3+bx2+cx+d的大致图象,则x12+x22等于( )


| A. | $\frac{16}{9}$ | B. | $\frac{10}{9}$ | C. | $\frac{8}{9}$ | D. | $\frac{28}{9}$ |
9.已知函数f(x)=xlnx,则下列说法正确的是( )
| A. | f (x)在(0,+∞)上单调递增 | B. | f (x)在(0,+∞)上单调递减 | ||
| C. | f (x)在(0,$\frac{1}{e}$)上单调递增 | D. | f (x)在(0,$\frac{1}{e}$)上单调递减 |
16.已知函数f(x)为R上的减函数,则满足$f({(\frac{1}{2})^x})$>f(1)的实数x的取值范围是( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (0,1)∪(1,+∞) | D. | (0,1) |