题目内容
9.已知函数f(x)=xlnx,则下列说法正确的是( )| A. | f (x)在(0,+∞)上单调递增 | B. | f (x)在(0,+∞)上单调递减 | ||
| C. | f (x)在(0,$\frac{1}{e}$)上单调递增 | D. | f (x)在(0,$\frac{1}{e}$)上单调递减 |
分析 求得f′(x)=1+lnx,f′(x)=0得:x=$\frac{1}{e}$;由f′(x)<0可求其单调递减区间,由f′(x)>0,可求其单调递增区间,从而得到答案.
解答 解:∵f′(x)=lnx+x•$\frac{1}{x}$=1+lnx,由f′(x)=0得:x=$\frac{1}{e}$;
当0<x<$\frac{1}{e}$,f′(x)<0,
∴f(x)在(0,$\frac{1}{e}$)上单调递减;
当x>$\frac{1}{e}$,f′(x)>0,
f(x)在($\frac{1}{e}$,+∞)上单调递增;
故选:D.
点评 本题考查利用导数研究函数的单调性,求得f′(x)=1+lnx是基础,由f′(x)的符号判断单调区间是关键,属于中档题.

练习册系列答案
相关题目
19.直线y=x-2与圆x2+y2-4x+3=0交于A、B两点,与抛物线y2=8x交于C、D两点,则|AB|+|CD|=( )
| A. | 16 | B. | 14 | C. | 18 | D. | $14\sqrt{2}$ |
4.函数y=sinx在[-π,π]上的图象是( )
| A. |  | B. |  | C. |  | D. | 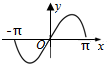 |
14.设集合A={x|2x+1<3x},B={x|-3<x<2},则A∩B等于( )
| A. | {x|-3<x<1} | B. | {x|1<x<2} | C. | {x|x>-3} | D. | {x|x<1} |
1.已知a>0,b>0,且a+b=1,则ab( )
| A. | 有最小值$\frac{1}{4}$ | B. | 有最大值$\frac{1}{4}$ | C. | 有最小值$\frac{1}{2}$ | D. | 有最大值$\frac{1}{2}$ |