题目内容
19.如图是函数f(x)=x3+bx2+cx+d的大致图象,则x12+x22等于( )
| A. | $\frac{16}{9}$ | B. | $\frac{10}{9}$ | C. | $\frac{8}{9}$ | D. | $\frac{28}{9}$ |
分析 解:由图象知f(-1)=f(0)=f(2)=0,解出 b、c、d的值,由x1和x2是f′(x)=0的根,使用根与系数的关系得到x1+x2=$\frac{2}{3}$,x1•x2=-$\frac{2}{3}$,则由x12+x22 =(x1+x2)2-2x1•x2 代入可求得结果.
解答 解:∵f(x)=x3+bx2+cx+d,由图象知,-1+b-c+d=0,0+0+0+d=0,
8+4b+2c+d=0,∴d=0,b=-1,c=-2
∴f′(x)=3x2+2bx+c=3x2-2x-2. 由题意有x1和x2是函数f(x)的极值,
故有x1和x2是f′(x)=0的根,∴x1+x2=$\frac{2}{3}$,x1•x2=-$\frac{2}{3}$.
则x12+x22 =(x1+x2)2-2x1•x2=$\frac{4}{9}$+$\frac{4}{3}$=$\frac{16}{9}$
故选:A.
点评 本题考查一元二次方程根的分布,根与系数的关系,函数在某点取的极值的条件,以及求函数的导数,属中档题.

练习册系列答案
相关题目
9.在△ABC中,若b=2asinB,则A等( )
| A. | 30° | B. | 60° | C. | 120°或60° | D. | 30°或150° |
10.一个由十个数字组成的密码的前八个数字为1,1,2,3,5,8,1,3,请你推测最后的两个数字最有可能是( )
| A. | 2,1 | B. | 2,0 | C. | 1,3 | D. | 3,1 |
4.函数y=sinx在[-π,π]上的图象是( )
| A. |  | B. |  | C. |  | D. | 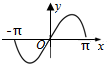 |
9.计算i+i2+i3+…i2015=( )
| A. | 1 | B. | i | C. | -i | D. | -1 |