题目内容
16.已知函数f(x)为R上的减函数,则满足$f({(\frac{1}{2})^x})$>f(1)的实数x的取值范围是( )| A. | (-∞,0) | B. | (0,+∞) | C. | (0,1)∪(1,+∞) | D. | (0,1) |
分析 根据函数单调性的性质进行求解即可.
解答 解:∵函数f(x)为R上的减函数,
∴若满足$f({(\frac{1}{2})^x})$>f(1),
则$(\frac{1}{2})^{x}<1$,即x>0,
故选:B
点评 本题主要考查函数单调性的应用,比较基础.

练习册系列答案
相关题目
6.一个学校高三年级共有学生200人,其中男生有120人,女生有80人.为了调查高三复习状况,用分层抽样的方法从全体高三学生中抽取一个容量为25的样本,应抽取女生的人数为( )
| A. | 15 | B. | 20 | C. | 10 | D. | 8 |
4.函数y=sinx在[-π,π]上的图象是( )
| A. |  | B. |  | C. |  | D. | 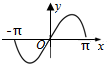 |
1.已知a>0,b>0,且a+b=1,则ab( )
| A. | 有最小值$\frac{1}{4}$ | B. | 有最大值$\frac{1}{4}$ | C. | 有最小值$\frac{1}{2}$ | D. | 有最大值$\frac{1}{2}$ |