题目内容
12.已知幂函数f(x)=kxa(k∈R,a∈R)的图象经过点($\frac{1}{2},\frac{1}{4}$),则k+a=3;函数y=$\sqrt{3-2x-f(x)}$的定义域为[-3,1].分析 利用幂函数的定义求出k,利用函数的图象经过的点求出α,即可得到结果,再根据二次根式,得到3-2x-x2≥0,解得即可.
解答 解:因为幂函数f(x)=k•xα(k,α∈R)
由幂函数的定义可知k=1,
幂函数f(x)=k•xα(k,α∈R)的图象过点$({\frac{1}{2},\frac{1}{4}})$,
∴$\frac{1}{4}$=($\frac{1}{2}$)α,解得α=2,
∴k+α=3,
∴f(x)=x2,
∵$y=\sqrt{3-2x-f(x)}$,
∴3-2x-x2≥0,
解得-3≤x≤1,
所以函数$y=\sqrt{3-2x-f(x)}$的定义域为为[-3,1].
故答案为:3;[-3,1].
点评 本题考查了幂函数的图象和性质,以及一元二次不等式的解法,属于基础题.

练习册系列答案
相关题目
2.已知f(x+1)=x-1+ex+1,则函数f(x)在点(0,f(0))处的切线与坐标轴围成的三角形的面积为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
4.函数y=sinx在[-π,π]上的图象是( )
| A. |  | B. |  | C. |  | D. | 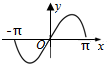 |
1.已知a>0,b>0,且a+b=1,则ab( )
| A. | 有最小值$\frac{1}{4}$ | B. | 有最大值$\frac{1}{4}$ | C. | 有最小值$\frac{1}{2}$ | D. | 有最大值$\frac{1}{2}$ |