题目内容
【题目】(12分)在数列![]() 中,对于任意
中,对于任意![]() ,等式
,等式![]()
成立,其中常数![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求证:数列![]() 为等比数列;
为等比数列;
(Ⅲ)如果关于n的不等式![]() 的解集为
的解集为
![]() ,求b和c的取值范围.
,求b和c的取值范围.
【答案】(1)![]() ,
, ![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() ,
, ![]() .
.
【解析】试题分析:(1)分别取n=1,n=2代入![]() ,即可得;(2)要证明数列
,即可得;(2)要证明数列![]() 为等比数列,先求出
为等比数列,先求出![]() ,为此由已知写出
,为此由已知写出![]() ,两式相减,即可求出
,两式相减,即可求出![]() ,再用等比数列的定义证明数列
,再用等比数列的定义证明数列![]() 为等比数列.(3)先求出
为等比数列.(3)先求出![]() 的和,不等式转化为
的和,不等式转化为![]() ,再对b进行分类讨论,进一步转化为
,再对b进行分类讨论,进一步转化为![]() 或
或![]() ,再由不等式的解集确定出求b和c的取值范围.
,再由不等式的解集确定出求b和c的取值范围.
试题解析:
(Ⅰ)解:因为![]() ,
,
所以![]() ,
, ![]() ,
,
解得 ![]() ,
, ![]() .
.
(Ⅱ)证明:当![]() 时,由
时,由![]() , ①
, ①
得![]() , ②
, ②
将①,②两式相减,得 ![]() ,
,
化简,得![]() ,其中
,其中![]() .
.
因为![]() ,
,
所以 ![]() ,其中
,其中![]() .
.
因为 ![]() 为常数,
为常数,
所以数列![]() 为等比数列.
为等比数列.
(Ⅲ)解:由(Ⅱ),得![]() ,
,
所以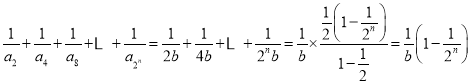 , 11分
, 11分
又因为![]() ,
,
所以不等式![]()
![]() 化简为
化简为![]() ,
,
当![]() 时,考察不等式
时,考察不等式![]() 的解,
的解,
由题意,知不等式![]() 的解集为
的解集为![]() ,
,
因为函数![]() 在R上单调递增,
在R上单调递增,
所以只要求 ![]() 且
且![]() 即可,
即可,
解得![]() ;
;
当![]() 时,考察不等式
时,考察不等式![]() 的解,
的解,
由题意,要求不等式![]() 的解集为
的解集为![]() ,
,
因为![]() ,
,
所以如果![]() 时不等式成立,那么
时不等式成立,那么![]() 时不等式也成立,
时不等式也成立,
这与题意不符,舍去.
所以![]() ,
, ![]() .
.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案【题目】现在很多人喜欢自助游,2017年孝感杨店桃花节,美丽的桃花风景和人文景观迎来众多宾客.某调查机构为了了解“自助游”是否与性别有关,在孝感桃花节期间,随机抽取了![]() 人,得如下所示的列联表:
人,得如下所示的列联表:
赞成“自助游” | 不赞成“自助游” | 合计 | |
男性 |
| ||
女性 |
| ||
合计 |
|
(1)若在![]() 这人中,按性别分层抽取一个容量为
这人中,按性别分层抽取一个容量为![]() 的样本,女性应抽
的样本,女性应抽![]() 人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过
人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过![]() 前提下,认为赞成“自助游”是与性别有关系?
前提下,认为赞成“自助游”是与性别有关系?
(2)若以抽取样本的频率为概率,从旅游节大量游客中随机抽取![]() 人赠送精美纪念品,记这
人赠送精美纪念品,记这![]() 人中赞成“自助游”人数为
人中赞成“自助游”人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附: 
|
|
|
|
|
|
|
|
|
|