题目内容
已知线段AB的两个端点A,B分别在x轴、y轴上滑动,|AB|=3,点M满足2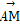 =
= .
.
(1)求动点M的轨迹E的方程.
(2)若曲线E的所有弦都不能被直线l:y=k(x-1)垂直平分,求实数k的取值范围.
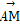 =
= .
.(1)求动点M的轨迹E的方程.
(2)若曲线E的所有弦都不能被直线l:y=k(x-1)垂直平分,求实数k的取值范围.
(1)  +y2=1 (2) k≤-
+y2=1 (2) k≤-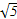 或k≥
或k≥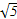 .
.
 +y2=1 (2) k≤-
+y2=1 (2) k≤-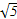 或k≥
或k≥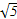 .
.(1)设M(x,y),A(x0,0),B(0,y0),
则 +
+ =9,
=9,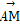 =(x-x0,y),
=(x-x0,y), =(-x,y0-y).
=(-x,y0-y).
由2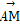 =
= ,得
,得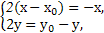 解得
解得
代入 +
+ =9,
=9,
化简得点M的轨迹方程为 +y2=1.
+y2=1.
(2)由题意知k≠0,
假设存在弦CD被直线l垂直平分,设直线CD的方程为y=- x+b,
x+b,
由 消去y化简得
消去y化简得
(k2+4)x2-8kbx+4k2(b2-1)=0,
Δ=(-8kb)2-4(k2+4)·4k2(b2-1)
=-16k2(k2b2-k2-4)>0,
k2b2-k2-4<0,
设C(x1,y1),D(x2,y2),CD中点P(xp,yp),
则x1+x2= ,
,
xp= =
=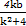 ,
,
yp=- xp+b=-
xp+b=- ·
·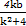 +b=
+b= ,
,
又yp=k(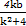 -1),
-1),
∴k(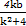 -1)=
-1)= ,得b=
,得b= ,
,
代入k2b2-k2-4<0,得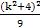 -(k2+4)<0,
-(k2+4)<0,
解得k2<5,∴-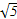 <k<
<k<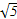 .
.
∴当曲线E的所有弦都不能被直线l:y=k(x-1)垂直平分时,k的取值范围是k≤-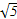 或k≥
或k≥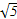 .
.
则
 +
+ =9,
=9,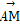 =(x-x0,y),
=(x-x0,y), =(-x,y0-y).
=(-x,y0-y).由2
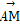 =
= ,得
,得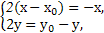 解得
解得
代入
 +
+ =9,
=9,化简得点M的轨迹方程为
 +y2=1.
+y2=1.(2)由题意知k≠0,
假设存在弦CD被直线l垂直平分,设直线CD的方程为y=-
 x+b,
x+b,由
 消去y化简得
消去y化简得(k2+4)x2-8kbx+4k2(b2-1)=0,
Δ=(-8kb)2-4(k2+4)·4k2(b2-1)
=-16k2(k2b2-k2-4)>0,
k2b2-k2-4<0,
设C(x1,y1),D(x2,y2),CD中点P(xp,yp),
则x1+x2=
 ,
,xp=
 =
=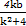 ,
,yp=-
 xp+b=-
xp+b=- ·
·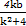 +b=
+b= ,
,又yp=k(
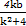 -1),
-1),∴k(
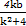 -1)=
-1)= ,得b=
,得b= ,
,代入k2b2-k2-4<0,得
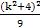 -(k2+4)<0,
-(k2+4)<0,解得k2<5,∴-
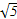 <k<
<k<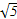 .
.∴当曲线E的所有弦都不能被直线l:y=k(x-1)垂直平分时,k的取值范围是k≤-
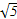 或k≥
或k≥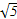 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 +
+ =1(a>b>0)的焦距等于2|ON|,且过点(
=1(a>b>0)的焦距等于2|ON|,且过点( ,
, ).
).
 +
+ =1(a>b>0)的右焦点为F(1,0),且点(-1,
=1(a>b>0)的右焦点为F(1,0),且点(-1,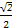 )在椭圆C上.
)在椭圆C上. ,0),动直线l过点F,且直线l与椭圆C交于A,B两点,证明:
,0),动直线l过点F,且直线l与椭圆C交于A,B两点,证明: ·
· 为定值.
为定值. ,且过点M
,且过点M 。
。 的直线l交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由。
的直线l交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由。 的焦点
的焦点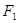 、
、 ,点
,点 为其上的动点,当∠
为其上的动点,当∠ +
+ =1(a>b>0)上的任意一点,F1为椭圆的一个焦点,则|PF1|的取值范围为 .
=1(a>b>0)上的任意一点,F1为椭圆的一个焦点,则|PF1|的取值范围为 . +y2=1截得的最大弦长是( )
+y2=1截得的最大弦长是( )


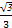

 +y2=1,在椭圆C上任取不同两点A,B,点A关于x轴的对称点为A′,当A,B变化时,如果直线AB经过x轴上的定点T(1,0),则直线A′B经过x轴上的定点为________.
+y2=1,在椭圆C上任取不同两点A,B,点A关于x轴的对称点为A′,当A,B变化时,如果直线AB经过x轴上的定点T(1,0),则直线A′B经过x轴上的定点为________.