题目内容
已知曲线C上的动点M(x,y),向量a=(x+2,y)和b=(x-2,y)满足|a|+|b|=6,则曲线C的离心率是( )
A． | B． | C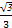． | D． |
A
因为|a|+|b|=6表示动点M(x,y)到两点(-2,0)和(2,0)距离的和为6,所以曲线C是椭圆,且长轴长2a=6,即a=3,
又c=2,∴e=.
又c=2,∴e=
.
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
| A． | B． | C． | D． |
.阅读快车系列答案
到定点
与到定直线,
的距离之比为 
． 
的轨迹方程；
（与x轴不重合）与（1）中轨迹交于两点
、
.探究是否存在一定点E(t，0)，使得x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等？若存在，求出t的值；若不存在，说明理由．
+
=1(a>b>0)的离心率为
.双曲线x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
+
=1
+
=1
+
=1
+
=1
上斜率为1的弦的中点在直线
上，类比上述结论：双曲线
上斜率为1的弦的中点在直线 上
=
.
+
＝1(a＞b＞0)的右焦点为F(3,0)，过点F的直线交E于A，B两点．若AB的中点坐标为(1，－1)，则E的方程为( )
＝1 
＝1 
＝1 
＝1
的一个焦点坐标是（ ）
＝λ，求点M的轨迹方程，并说明轨迹是什么曲线．