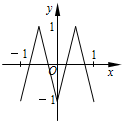题目内容

8．设集合A={x|x2-6x+8＜0}，B={x|2＜2x＜8}，则A∩B=（　　）
A．{x|1＜x＜4}B．{x|1＜x＜3}C．{x|2＜x＜3}D．{x|3＜x＜4}

分析 求出集合的等价条件，利用集合的基本运算进行求解即可．

解答 解：A={x|x2-6x+8＜0}={x|2＜x＜4}，
B={x|2＜2x＜8}={x|1＜x＜3}，
则A∩B={x|2＜x＜3}，
故选：C．

点评 本题主要考查集合的基本运算，求出集合的等价条件是解决本题的关键．

练习册系列答案
相关题目
18．要得到函数y=tan（3x+$\frac{π}{3}$）的图象，只须将x=tan3x的图象上的所有的点（　　）
A．向左平移$\frac{π}{3}$个单位长度B．向右平移$\frac{π}{3}$个单位长度
C．向左平移$\frac{π}{9}$个单位长度D．向右平移$\frac{π}{9}$个单位长度
19．已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左右焦点为F1，F2，点A（x1，y1），B（x2，y2）在椭圆上，若x1+x2=$\frac{1}{2}$，且$\overrightarrow{A{F}_{2}}$=λ$\overrightarrow{{F}_{2}B}$，求λ的值．
16．当m为何实数时，方程（m+2）x2-2mx+1=0有两个不相等的实数根？
3．已知正项等比数列{an}满足a7=a6+2a5，若am，an满足$\sqrt{{a}_{m}{a}_{n}}$=8a1，则$\frac{1}{m}$+$\frac{9}{n}$的最小值为（　　）
A．2B．4C．6D．8
13．已知$\frac{1+tan（π+α）}{1+tan（2π-α）}$=-3，求cos2（π-α）+sin（$\frac{3π}{2}$+α）•cos（$\frac{π}{2}$+α）+2sin2（α-π）的值．
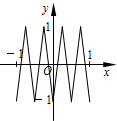
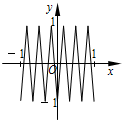
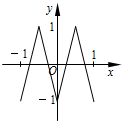20．如图，函数y=f（x）的图象为折线ABC，设f1（x）=f（x），fn+1（x）=f[fn（x）]，n∈N*，则函数y=f4（x）的图象为（　　）
A．B．C．D．
17．若集合A={2，0}，B={1，5}，则A∩B=（　　）
A．∅B．{0}C．{0，1}D．{2，0，1，5}
18．若x，y满足$\left\{\begin{array}{l}x-y≥0\\ x+y≤2\\ y≥0\end{array}\right.$，则目标函数z=x+2y的最大值为3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网