题目内容
2.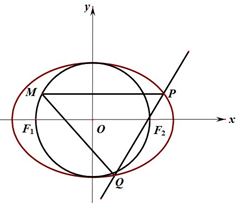 如图,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2做直线l交椭圆于P,Q两点.若圆O:x2+y2=b2过F1,F2,且△PF1F2的周长为2$\sqrt{2}$+2.
如图,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2做直线l交椭圆于P,Q两点.若圆O:x2+y2=b2过F1,F2,且△PF1F2的周长为2$\sqrt{2}$+2.(Ⅰ)求椭圆C和圆O的方程;
(Ⅱ)若M为圆O上任意一点,设直线l的方程为4x-3y-4=0,求△MPQ面积S△MPQ的最大值.
分析 (Ⅰ)通过$\left\{\begin{array}{l}{2a+2c=2\sqrt{2}+2}\\{c=b}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,计算即得结论;
(Ⅱ)设P(x1,y1),Q(x2,y2),将直线l方程代入椭圆方程,利用韦达定理及两点间距离公式可得|PQ|=$\frac{50\sqrt{2}}{41}$,易知点M到直线l的距离最大时S△MPQ最大,计算即得结论.
解答 解:(Ⅰ)由已知可得$\left\{\begin{array}{l}{2a+2c=2\sqrt{2}+2}\\{c=b}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,
解得:b=c=1,a=$\sqrt{2}$,
∴椭圆C方程为:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
圆O的方程:x2+y2=1;
(Ⅱ)设P(x1,y1),Q(x2,y2),
将直线l方程代入椭圆方程得:y1+y2=-$\frac{24}{41}$,y1y2=-$\frac{16}{41}$,
∴|PQ|=$\sqrt{1+(\frac{3}{4})^{2}}$•|y1-y2|=$\frac{50\sqrt{2}}{41}$,
为使S△MPQ最大,只需点M到直线l的距离最大,
最大距离等于圆心到直线l的距离与圆半径之和,即h=$\frac{4}{5}$+1=$\frac{9}{5}$,
∴(S△MPQ)max=$\frac{1}{2}$|PQ|•h=$\frac{45\sqrt{2}}{41}$.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
19.已知某几何体的三视图(单位:cm),如图所示,则此几何体的外接球的体积为( )
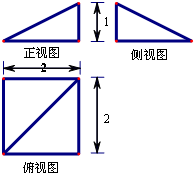

| A. | $\frac{9}{2}$πcm3 | B. | 36πcm3 | C. | $\frac{64}{3}$πcm3 | D. | 9πcm3 |