题目内容
7.已知函数f(x)=$\frac{{a}^{x}-1}{{a}^{x}+1}$(a>1)(Ⅰ)判断函数f(x)的奇偶性
(Ⅱ)判断f(x)在(-∞,+∞)上的单调性,并用定义证明.
分析 (Ⅰ)由题意可得函数的定义域为R,可得f(-x)=-f(x),可得奇函数;
(Ⅱ)设x1,x2∈(-∞,+∞)且x1<x2,可判定f(x1)-f(x2)的符号,由单调性的定义可得结论.
解答 解:(Ⅰ)可得函数的定义域为R,
f(-x)=$\frac{{a}^{-x}-1}{{a}^{-x}+1}$=$\frac{1-{a}^{x}}{1+{a}^{x}}$=-$\frac{{a}^{x}-1}{{a}^{x}+1}$=-f(x),
∴函数f(x)为奇函数;
(Ⅱ)函数f(x)在(-∞,+∞)为增函数,证明如下:
设x1,x2∈(-∞,+∞)且x1<x2,
则f(x1)-f(x2)=$\frac{{a}^{{x}_{1}}-1}{{a}^{{x}_{1}}+1}$-$\frac{{a}^{{x}_{2}}-1}{{a}^{{x}_{2}}+1}$
=$\frac{({a}^{{x}_{1}}-1)({a}^{{x}_{2}}+1)-({a}^{{x}_{2}}-1)({a}^{{x}_{1}+1})}{({a}^{{x}_{1}}+1)({a}^{{x}_{2}}+1)}$=$\frac{2({a}^{{x}_{1}}-{a}^{{x}_{2}})}{({a}^{{x}_{1}}+1)({a}^{{x}_{2}}+1)}$,
∵a>1且x1<x2,∴${a}^{{x}_{1}}$-${a}^{{x}_{2}}$<0,∴$\frac{2({a}^{{x}_{1}}-{a}^{{x}_{2}})}{({a}^{{x}_{1}}+1)({a}^{{x}_{2}}+1)}$<0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在(-∞,+∞)上是增函数.
点评 本题考查函数的单调性和奇偶性,涉及单调性的定义法证明,属基础题.

| A. | f(x)=0是常值函数中唯一一个“t型函数” | |
| B. | f(x)=x2是一个“t型函数” | |
| C. | f(x)=|x-$\frac{1}{2}$|是一个“t型函数” | |
| D. | “$\frac{1}{2}$型函数”至少有一个零点 |
| A. | ?x≤0,lnx≥x | B. | ?x>0,lnx≥x | C. | ?x≤0,lnx<x | D. | ?x>0,lnx<x |
| A. | $\frac{4}{9}$ | B. | -$\frac{4}{9}$ | C. | $\frac{9}{4}$ | D. | -$\frac{9}{4}$ |
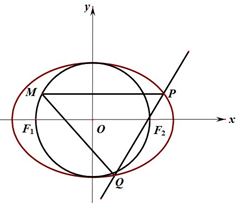 如图,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2做直线l交椭圆于P,Q两点.若圆O:x2+y2=b2过F1,F2,且△PF1F2的周长为2$\sqrt{2}$+2.
如图,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2做直线l交椭圆于P,Q两点.若圆O:x2+y2=b2过F1,F2,且△PF1F2的周长为2$\sqrt{2}$+2.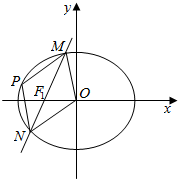 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为$\frac{{4\sqrt{3}}}{3}$,且$a=\sqrt{2}b$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为$\frac{{4\sqrt{3}}}{3}$,且$a=\sqrt{2}b$.