题目内容
14.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,离心率e为$\frac{1}{2}$,过F1的直线l1与椭圆C交于M,N两点,且△MNF2的周长为8.(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l2与椭圆C交于A,B两点,O为坐标原点,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=0.过点O作直线l2的垂线,垂足为Q,求点Q的轨迹方程.
分析 (I)利用已知条件求出a,b,然后求解椭圆C的方程.
(II)利用条件得到OA⊥OB.(1)若直线l2的斜率不存在,则点Q在x轴上.设点Q的坐标为(x0,0),则A(x0,x0),B(x0,-x0).然后求出点Q的轨迹方程.(2)若直线l2,的斜率存在,设直线l2的方程为:y=kx+m,联立直线与椭圆方程,设A(x1,y1),B(x2,y2),利用韦达定理以及OA⊥OB,整理得7m2=12(k2+1),然后求出点Q的轨迹方程.
解答 解:(I)由题意知,4a=8,所以a=2. …(2分)
∵$e=\frac{1}{2}$,∴c=1,b2=3. …(3分)
∴椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$. …(4分)
(II)∵$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,∴OA⊥OB.
(1)若直线l2的斜率不存在,则点Q在x轴上.
设点Q的坐标为(x0,0),则A(x0,x0),B(x0,-x0).
又∵A,B两点在椭圆C上,∴$\frac{{{x_0}^2}}{4}+\frac{{{x_0}^2}}{3}=1$,${x_0}^2=\frac{12}{7}$.
∴点Q的坐标为$(±\sqrt{\frac{12}{7}},0)$,即$|OQ|=\sqrt{\frac{12}{7}}$. …(6分)
(2)若直线l2,的斜率存在,设直线l2的方程为:y=kx+m,
由$\left\{\begin{array}{l}y=kx+m\\ \frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1\end{array}\right.$,消去y可得:(3+4k2)x2+8kmx+4m2-12=0,
由△>0可得,m2<3+4k2.
设A(x1,y1),B(x2,y2),则${x_1}+{x_2}=-\frac{8km}{{3+4{k^2}}}$,${x_1}{x_2}=\frac{{4{m^2}-12}}{{3+4{k^2}}}$.…(8分)
∵OA⊥OB,∴x1x2+y1y2=0.
∴x1x2+(kx1+m)(kx2+m)=0,即$({k^2}+1){x_1}{x_2}+km({x_1}+{x_2})+{m^2}=0$.
∴$({k^2}+1)\frac{{4{m^2}-12}}{{3+4{k^2}}}-\frac{{8{k^2}{m^2}}}{{3+4{k^2}}}+{m^2}=0$.
整理得7m2=12(k2+1),满足m2<3+4k2.…(9分)
又由已知可得,过原点O与直线l2垂直的直线方程为$y=-\frac{1}{k}x$,
解方程组$\left\{\begin{array}{l}y=-\frac{1}{k}x\\ y=kx+m\end{array}\right.$得点Q的横坐标与纵坐标分别为$x=-\frac{k}{{{k^2}+1}}m,y=\frac{1}{{{k^2}+1}}m$,
∴${x^2}+{y^2}=\frac{k^2}{{{{({k^2}+1)}^2}}}{m^2}+\frac{1}{{{{({k^2}+1)}^2}}}{m^2}=\frac{m^2}{{{k^2}+1}}=\frac{12}{7}$.即$|OQ|=\sqrt{\frac{12}{7}}$.…(11分)
综合(1)、(2)可知,点Q的轨迹是以坐标原点为圆心,半径为$\sqrt{\frac{12}{7}}$的一个圆,
且该圆的方程为:${x^2}+{y^2}=\frac{12}{7}$.…(12分)
点评 本题考查椭圆方程的求法,直线与椭圆的位置关系的综合应用,考查分类讨论思想,分析问题解决问题的能力,转化思想的应用.

| A. | {3} | B. | {x|x≤2,或x=3} | ||
| C. | {x|x<-2或-2<x≤2,或x=3} | D. | {x|x<-2,或-2<x≤2} |
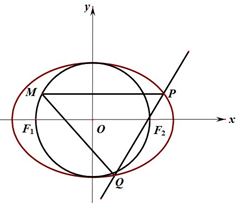 如图,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2做直线l交椭圆于P,Q两点.若圆O:x2+y2=b2过F1,F2,且△PF1F2的周长为2$\sqrt{2}$+2.
如图,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2做直线l交椭圆于P,Q两点.若圆O:x2+y2=b2过F1,F2,且△PF1F2的周长为2$\sqrt{2}$+2.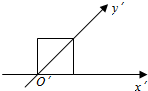 用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个边长为1的正方形,则原来的图形的面积是2$\sqrt{2}$.
用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个边长为1的正方形,则原来的图形的面积是2$\sqrt{2}$.