题目内容

11．设复数z=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i，则满足zn=z的大于1的正整数n中，最小是（　　）
A．7B．4C．3D．2

分析 直接利用复数的乘法运算法则求解即可．

解答 解：复数z=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i，则z2=（-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i）2=-$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i．
z3=（-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i）2（-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i）=（-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i）（-$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i）=1．
z4=z3z=z．
复数z=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i，则满足zn=z的大于1的正整数n中，最小是4．
故选：B．

点评 本题考查1的立方虚根的应用，复数的乘法运算法则的应用，基本知识的考查．

练习册系列答案
相关题目
3．某单位要从甲、乙、丙、丁四支门球队中选拔两支参加上级比赛，选拔赛采用单循环制（即每两个队比赛一场），并规定积分前两名的队出线，其中胜一场积3分，平一场积1分，负一场积0分．在经过三场比赛后，目前的积分状况如下：甲队积7分，乙队积1分，丙和丁队各积0分．根据以往的比赛情况统计：
 乙队胜的概率乙队平的概率乙队负的概率
与丙 队比赛$\frac{1}{4}$$\frac{1}{4}$$\frac{1}{2}$
与丁队比赛$\frac{1}{3}$$\frac{1}{3}$$\frac{1}{3}$
注：各队之间比赛结果相互独立．
（Ⅰ）选拔赛结束，求乙队积4分的概率；
（Ⅱ）设随机变量X为选拔赛结束后乙队的积分，求随机变量X的分布列与数学期望；
（Ⅲ）在目前的积分情况下，M同学认为：乙队至少积4分才能确保出线，N同学认为：乙队至少积5分才能确保出线．你认为谁的观点对？或是两者都不对？（直接写结果，不需证明）
2．如图，设椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1，F2，过F2做直线l交椭圆于P，Q两点．若圆O：x2+y2=b2过F1，F2，且△PF1F2的周长为2$\sqrt{2}$+2．
（Ⅰ）求椭圆C和圆O的方程；
（Ⅱ）若M为圆O上任意一点，设直线l的方程为4x-3y-4=0，求△MPQ面积S△MPQ的最大值．
19．已知等差数列{an}的公差d＞0，前n项和为Sn，且a1=2，S2•S3=$\frac{112}{3}$．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若从{an}中抽取一个公比为q的等比数列{a${\;}_{{k}_{n}}$}，其中k1=1，且k1＜k2＜…＜kn＜…，kn∈N*，求满足条件的最小q值．
6．已知集合A={x|0≤$\sqrt{{x}^{2}}$≤1}，B={x|-p≤x≤p}，要使A=B，则p的值为1．
16．等比数列{an}的前n 项和为Sn，已知S1，S3，S2成等差数列
（1）求{an}的公比q；
（2）若a1-a3=3，bn=nan．求数列{bn}的前n 项和Tn．
3．已知函数f（x）=$\frac{sinx}{{e}^{x}}$．
（1）求函数f（x）的单调区间；
（2）如果对于任意的x∈[-$\frac{π}{2}$，0]，f（x）≤kx恒成立，求实数k的取值范围．
20．一个几何体的三视图如图所示（单位：m），则该几何体的表面积为（单位：m2）（　　）
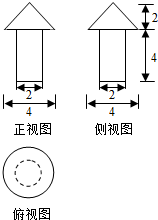
A．（11+$4\sqrt{2}$）πB．（12+4$\sqrt{2}$）πC．（13+4$\sqrt{2}$）πD．（14+4$\sqrt{2}$）π
1．四棱锥S-ABCD中，底面ABCD是边长为2$\sqrt{3}$的正方形，SA⊥平面ABCD，且SA=2$\sqrt{6}$，则此四棱锥的外接球的表面积为（　　）
A．12πB．24πC．144πD．48π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网