题目内容
16.下列命题中正确的是( )①“若x2+y2≠0,则x,y不全为零”;
②“正三角形都相似”的逆命题;
③“若m>0,则x2+x-m=0有实根”的逆否命题;
④在实数范围内,“若x-$\sqrt{2}$是有理数,则x是无理数”的否命题.
| A. | ①②③④ | B. | ①③ | C. | ②③ | D. | ①④ |
分析 对于①“若x2+y2≠0,则x,y不全为零,可判断其真假;
对于②写出原命题“正三角形都相似”的逆命题,根据相似三角形的定义及正三角性的几何特征,可判断其真假;
对于③根据二次方程根的个数与△的符号的关系,判断原命题“若m>0,则x2+x-m=0有实根”的真假,进而根据互为逆否的两个命题真假性相同,可判断③的真假;
对于④写出原命题的否命题,举例即可判断,例如x=$\sqrt{3}$.
解答 解:对于①,“若x2+y2≠0,则x,y不全为零,故①是真命题;
对于②,“正三角形都相似”的逆命题为“相似的三角形都是正三角形”为假命题;
对于③,若m>0,则x2+x-m=0的△=1+4m>0,此时方程有实根,故原命题为真命题,故它的逆否命题也为真命题;
对于④,“若x-$\sqrt{2}$是有理数,则x是无理数”的否命题为“若x-$\sqrt{2}$不是有理数,则x不是无理数”为假命题.
故命题中正确的是①③.
故选:B
点评 本题以命题的真假判断为载体考查四种命题,熟练掌握互为逆否的两个命题真假性相同,及四种命题的定义是解答的关键.

练习册系列答案
相关题目
6.已知双曲线M的焦点与椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的焦点相同.如果直线y=-$\sqrt{2}$x是M的一条渐近线,那么M的方程为( )
| A. | $\frac{{x}^{2}}{18}$-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{18}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 | D. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{3}$=1 |
7.直线l:y=kx-1与圆x2+y2=1相交于A、B两点,则△OAB的面积最大值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
4.已知a=0.80.2,b=0.80.5,c=5.20.1,则这三个数的大小关系为( )
| A. | b<a<c | B. | a<b<c | C. | c<a<b | D. | c<b<a |
11.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的表面积是( )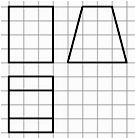

| A. | 42+6$\sqrt{17}$ | B. | 30+6$\sqrt{17}$ | C. | 66 | D. | 44 |
1. 如图,从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x 轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP,则椭圆的离心率为( )
如图,从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x 轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP,则椭圆的离心率为( )
 如图,从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x 轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP,则椭圆的离心率为( )
如图,从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x 轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP,则椭圆的离心率为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
8.在△ABC中,若C=90°,三边为a,b,c,则$\frac{a+b}{c}$的范围是( )
| A. | ($\sqrt{2}$,2) | B. | (1,$\sqrt{2}$] | C. | (0,$\sqrt{2}$] | D. | [$\frac{{\sqrt{2}}}{2}$,$\sqrt{2}$] |
5.设全集U=R,已知集合M={x|x2-x>0},N={x|$\frac{x-1}{x}$<0},则有( )
| A. | M∪N=R | B. | M∩N=∅ | C. | CuN=M | D. | CvM⊆N |
6.复数(1-4i)2的虚部为( )
| A. | -4i | B. | -4 | C. | -8i | D. | -8 |