题目内容
6.已知双曲线M的焦点与椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的焦点相同.如果直线y=-$\sqrt{2}$x是M的一条渐近线,那么M的方程为( )| A. | $\frac{{x}^{2}}{18}$-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{18}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 | D. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{3}$=1 |
分析 由题意可设双曲线的标准方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1(a,b>0)$,由直线y=-$\sqrt{2}$x是M的一条渐近线,可得$\frac{b}{a}$=$\sqrt{2}$.由椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的焦点为(±3,0),可得c=3,再利用c2=a2+b2,解出即可.
解答 解:由题意可设双曲线的标准方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1(a,b>0)$,
∵直线y=-$\sqrt{2}$x是M的一条渐近线,∴$\frac{b}{a}$=$\sqrt{2}$.
椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的焦点为(±3,0),
∴c=3,
联立$\left\{\begin{array}{l}{c=3}\\{\frac{b}{a}=\sqrt{2}}\\{{c}^{2}={a}^{2}+{b}^{2}}\end{array}\right.$,解得a2=3,b2=6.
∴M的方程为:$\frac{{x}^{2}}{3}-\frac{{y}^{2}}{6}=1$.
故选:C.
点评 本题考查了圆锥曲线的标准方程及其性质等基础知识与基本技能,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.已知向量$\overrightarrow{a}$={1,-1,2},$\overrightarrow{b}$={-2,2,m},且$\overrightarrow{a}$$∥\overrightarrow{b}$,则m的值为( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
5.已知函数f(x)=ex-ax有两个零点x1<x2,则下列说法错误的是( )
| A. | a>e | B. | x1+x2>2 | ||
| C. | x1x2>1 | D. | 有极小值点x0,且x1+x2<2x0 |
18.已知直线y=kx+1与椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{m}$=1恒有公共点,则实数m的取值范围为( )
| A. | m≥1 | B. | m≥1且m≠1 | C. | m≥1且m≠5 | D. | 0<m<5且m≠1 |
15.几何体的三视图如图,则其体积为( )
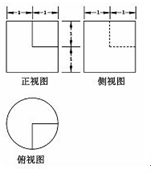

| A. | $\frac{3π}{2}$ | B. | $\frac{7π}{4}$ | C. | 2π-1 | D. | 4π-1 |