题目内容
7.直线l:y=kx-1与圆x2+y2=1相交于A、B两点,则△OAB的面积最大值为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
分析 由题意可得,△OAB的面积为$\frac{1}{2}$sin∠AOB,再根据正弦函数的值域,求得它的最大值.
解答 解:由题意可得OA=OB=1,△OAB的面积为$\frac{1}{2}$OA•OB•sin∠AOB=$\frac{1}{2}$sin∠AOB≤$\frac{1}{2}$,
故△OAB的面积最大值为$\frac{1}{2}$,
故选:B.
点评 本题主要考查直线和圆的位置关系,正弦函数的值域,属于基础题.

练习册系列答案
相关题目
18.已知直线y=kx+1与椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{m}$=1恒有公共点,则实数m的取值范围为( )
| A. | m≥1 | B. | m≥1且m≠1 | C. | m≥1且m≠5 | D. | 0<m<5且m≠1 |
15.几何体的三视图如图,则其体积为( )


| A. | $\frac{3π}{2}$ | B. | $\frac{7π}{4}$ | C. | 2π-1 | D. | 4π-1 |
16.下列命题中正确的是( )
①“若x2+y2≠0,则x,y不全为零”;
②“正三角形都相似”的逆命题;
③“若m>0,则x2+x-m=0有实根”的逆否命题;
④在实数范围内,“若x-$\sqrt{2}$是有理数,则x是无理数”的否命题.
①“若x2+y2≠0,则x,y不全为零”;
②“正三角形都相似”的逆命题;
③“若m>0,则x2+x-m=0有实根”的逆否命题;
④在实数范围内,“若x-$\sqrt{2}$是有理数,则x是无理数”的否命题.
| A. | ①②③④ | B. | ①③ | C. | ②③ | D. | ①④ |
17.某舰艇在A处测得遇险渔船在北偏东45°距离为10海里的C处,此时得知,该渔船沿北偏东105°方向,以每小时9海里的速度向一小岛靠近,舰艇时速21海里,则舰艇到达渔船的最短时间是( )小时.
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | 1 |
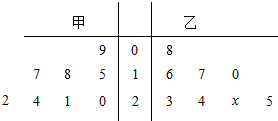 如图,茎叶图表示甲、乙两个篮球运动员在八场比赛中的得分,其中一个数字被污损,有x表示.
如图,茎叶图表示甲、乙两个篮球运动员在八场比赛中的得分,其中一个数字被污损,有x表示.