题目内容
已知数列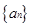 的前
的前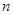 项和为
项和为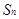 ,且满足:
,且满足: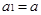
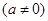 ,
,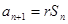
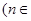 N*,
N*,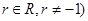 .
.
(1)求数列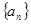 的通项公式;
的通项公式;
(2)若存在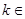 N*,使得
N*,使得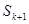 ,
,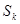 ,
,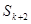 成等差数列,试判断:对于任意的
成等差数列,试判断:对于任意的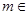 N*,且
N*,且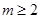 ,
,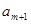 ,
,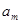 ,
,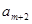 是否成等差数列,并证明你的结论.
是否成等差数列,并证明你的结论.
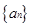 的前
的前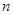 项和为
项和为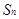 ,且满足:
,且满足: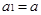
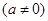 ,
,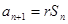
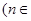 N*,
N*,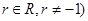 .
.(1)求数列
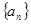 的通项公式;
的通项公式; (2)若存在
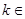 N*,使得
N*,使得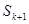 ,
,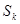 ,
,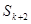 成等差数列,试判断:对于任意的
成等差数列,试判断:对于任意的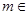 N*,且
N*,且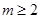 ,
,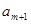 ,
,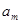 ,
,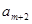 是否成等差数列,并证明你的结论.
是否成等差数列,并证明你的结论.(1)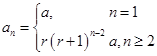
(2)对于任意的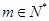 ,且
,且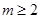 ,
,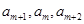 成等差数列
成等差数列
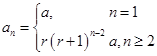
(2)对于任意的
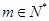 ,且
,且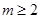 ,
,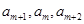 成等差数列
成等差数列(1)由已知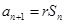 可得
可得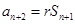 ,两式相减可得
,两式相减可得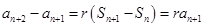 ,
,
即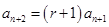 ,又
,又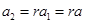 ,
,
所以当r=0时,数列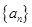 为a,0,0……,0,……;当
为a,0,0……,0,……;当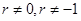 时,由已知
时,由已知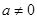 ,所以
,所以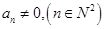 ,于是由
,于是由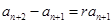 ,可得
,可得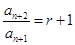 ,所以
,所以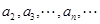 成等比数列,当
成等比数列,当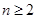 时,
时,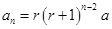 。
。
综上,数列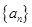 的通项公式为:
的通项公式为: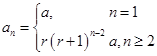 (6分)
(6分)
(2)对于任意的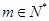 ,且
,且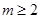 ,
,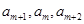 是否成等差数列,证明如下:
是否成等差数列,证明如下:
当r=0时,由(1),知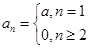 ,
,
故对于任意的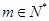 ,且
,且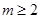 ,
,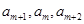 7成等差数列;
7成等差数列;
当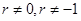 时,
时,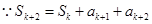 ,
,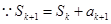 。
。
若存在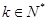 ,使得
,使得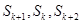 成等差数列,则
成等差数列,则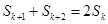 ,
,
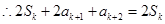 ,即
,即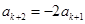 ,
,
由(1),知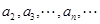 的公比
的公比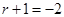 ,
,
于是对于任意的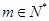 ,且
,且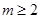 ,
,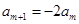 ,从而
,从而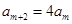 ,
,
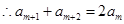 ,即
,即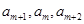 成等差数列。
成等差数列。
综上,对于任意的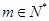 ,且
,且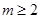 ,
,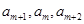 成等差数列。 (12分)
成等差数列。 (12分)
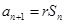 可得
可得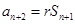 ,两式相减可得
,两式相减可得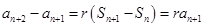 ,
,即
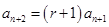 ,又
,又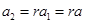 ,
,所以当r=0时,数列
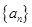 为a,0,0……,0,……;当
为a,0,0……,0,……;当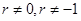 时,由已知
时,由已知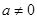 ,所以
,所以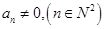 ,于是由
,于是由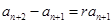 ,可得
,可得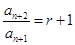 ,所以
,所以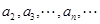 成等比数列,当
成等比数列,当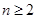 时,
时,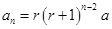 。
。综上,数列
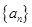 的通项公式为:
的通项公式为: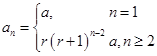 (6分)
(6分)(2)对于任意的
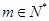 ,且
,且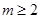 ,
,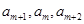 是否成等差数列,证明如下:
是否成等差数列,证明如下:当r=0时,由(1),知
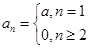 ,
,故对于任意的
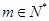 ,且
,且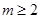 ,
,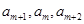 7成等差数列;
7成等差数列;当
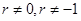 时,
时,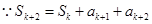 ,
,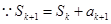 。
。若存在
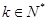 ,使得
,使得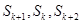 成等差数列,则
成等差数列,则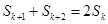 ,
,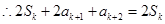 ,即
,即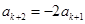 ,
,由(1),知
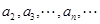 的公比
的公比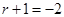 ,
,于是对于任意的
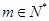 ,且
,且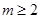 ,
,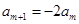 ,从而
,从而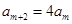 ,
,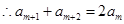 ,即
,即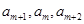 成等差数列。
成等差数列。综上,对于任意的
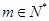 ,且
,且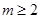 ,
,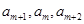 成等差数列。 (12分)
成等差数列。 (12分)
练习册系列答案
相关题目
 n-1+2(n∈N*),数列{bn}满足bn=2nan.
n-1+2(n∈N*),数列{bn}满足bn=2nan.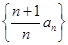 的前n项和为Tn,证明:n∈N*且n≥3时,Tn>
的前n项和为Tn,证明:n∈N*且n≥3时,Tn>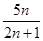 .
.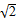 ,
,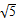 ,2
,2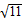 ,…,则2
,…,则2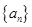 中,
中,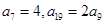 .
.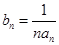 ,求数列
,求数列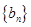 的前
的前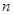 项和
项和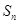 .
.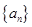 ,
,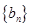 的前
的前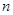 项和分别为
项和分别为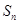 ,
,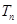 ,若
,若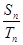 =
=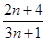 ,则
,则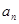 =
=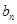 时
时 的前n项和
的前n项和 ,则
,则 的值为 ( )
的值为 ( )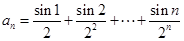 ,则对任意正整数
,则对任意正整数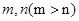 都成立的是( )
都成立的是( )