��Ŀ����
����Ŀ��ij����![]() ����
����![]() ��ũ������ͥ�˾�������
��ũ������ͥ�˾�������![]() ����λ��ǧԪ�������������
����λ��ǧԪ�������������
��� | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
��ݴ��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
�˾������� | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
��1����![]() ����
����![]() �����Իع鷽����
�����Իع鷽����
��2�����ã�1���еĻع鷽�̣�����![]() ����
����![]() ��õ���ũ������ͥ�˴�����ı仯�������Ԥ��õ���
��õ���ũ������ͥ�˴�����ı仯�������Ԥ��õ���![]() ��ũ������ͥ�˾�������.
��ũ������ͥ�˾�������.
�����ع�ֱ�ߵ�б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
 .
.
�ο����ݣ�![]() .
.
���𰸡�(1)![]() .
.
��2����![]() ����
����![]() ��õ��������ͥ�˾�����������������ƽ��ÿ������
��õ��������ͥ�˾�����������������ƽ��ÿ������![]() ǧԪ.
ǧԪ.
ԼΪ![]() ǧԪ.
ǧԪ.
��������������(1)�ɱ��е����ݿɷֱ���ù�ʽ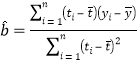 �еķ�������ĸ������
�еķ�������ĸ������![]() ��
��![]() �������ɵ�
�������ɵ�
![]() ��
��
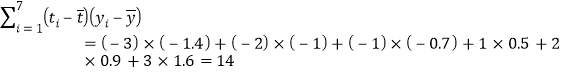 .���빫ʽ�������
.���빫ʽ�������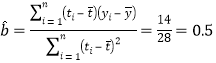 ������
������![]() ���
���![]() ����ûع鷽��Ϊ
����ûع鷽��Ϊ![]() . ��2���ɻع鷽��Ϊ
. ��2���ɻع鷽��Ϊ![]() .��
.��![]() ��ϵ��
��ϵ��![]() ����֪������Ϊ����أ������ɵ�
����֪������Ϊ����أ������ɵ�![]() ����
����![]() ��õ��������ͥ�˾��������������ӣ�ƽ��ÿ������
��õ��������ͥ�˾��������������ӣ�ƽ��ÿ������![]() ǧԪ��
ǧԪ��![]() �����ݴ���
�����ݴ���![]() ���ʿɽ�
���ʿɽ�![]() ����ع鷽��Ϊ
����ع鷽��Ϊ![]() .�����
.�����![]() ������Ԥ��õ���
������Ԥ��õ���![]() ��õ��������ͥ�˾�������ԼΪ
��õ��������ͥ�˾�������ԼΪ![]() ǧԪ.
ǧԪ.
�������1�����������ݼ����
![]() ��
��
![]() ��
��
![]() ��
��
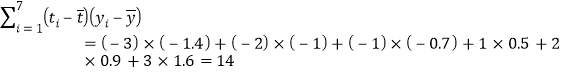 .
.
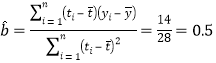 ��
��![]() ��
��
����ع鷽��Ϊ![]() .
.
��2���ɣ�1��֪��![]() ����
����![]() ����
����![]() ��õ��������ͥ�˾��������������ӣ�ƽ��ÿ������
��õ��������ͥ�˾��������������ӣ�ƽ��ÿ������![]() ǧԪ.
ǧԪ.
��![]() �����ݴ���
�����ݴ���![]() ���루1���Ļع鷽�̣���
���루1���Ļع鷽�̣���![]() ��
��
��Ԥ��õ���![]() ��õ��������ͥ�˾�������ԼΪ
��õ��������ͥ�˾�������ԼΪ![]() ǧԪ.
ǧԪ.