题目内容
【题目】某市对所有高校学生进行普通话水平测试，发现成绩服从正态分布N（μ，σ2），下表用茎叶图列举出来抽样出的10名学生的成绩．
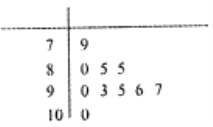
（1）计算这10名学生的成绩的均值和方差；
（2）给出正态分布的数据：P（μ﹣σ＜X＜μ+σ）=0.6826，P（μ﹣2σ＜X＜μ+2σ）=0.9544．
由（1）估计从全市随机抽取一名学生的成绩在（76，97）的概率．
【答案】（1）49（2）0.8185
【解析】分析：（1）根据茎叶图所给数据，求出总和，求得平均值；利用方差计算公式可得方差值。
（2）由3σ原则可知，成绩在（76，97）之间即在
之间的概率值，因而可求得概率值。
详解：（1）
=90，S2= 
=49
（2）由（1）可估计，μ=90，σ=7．
P（76＜x＜97）=P（μ﹣2σ＜x＜μ）+P（μ＜x＜μ+σ）= 
+ 
=0.8185
练习册系列答案
相关题目
【题目】某地区
年至
年农村居民家庭人均纯收入
（单位：千元）的数据如表：
年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入 | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
（1）求关于
的线性回归方程；
（2）利用（1）中的回归方程，分析年至年该地区农村居民家庭人纯收入的变化情况，并预测该地区
年农村居民家庭人均纯收入.
附：回归直线的斜率和截距的最小二乘估计公式分别为：
.
参考数据：
.
