Question

10．已知实数x，y满足条件$\left\{\begin{array}{l}{4{x}^{2}-{y}^{2}≥0}\\{x+ay+b≤0}\\{x≥0}\end{array}\right.$，z=x-y的最大值、最小值分别为M、m，且M-m=1，则a+b的取值范围为（　　）

• A． [$\frac{3\sqrt{3}}{2}$-2，$\frac{\sqrt{3}}{2}$）
• B． （-$\frac{1}{2}$，$\frac{1}{2}$）
• C． [$\sqrt{6}$-3，$\frac{1}{2}$）
• D． （$\frac{1}{2}$，$\frac{23}{10}$）

Answer 1

分析 由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解联立方程组求出最优解的坐标，代入目标函数求出M，m，由M-m=1把b用a表示，写出a+b，化为关于a的函数，利用函数的单调性求得a+b的取值范围．

解答 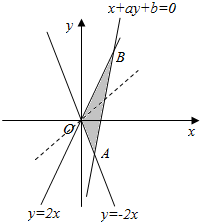解：由约束条件$\left\{\begin{array}{l}{4{x}^{2}-{y}^{2}≥0}\\{x+ay+b≤0}\\{x≥0}\end{array}\right.$作出可行域如图，
联立$\left\{\begin{array}{l}{y=2x}\\{x+ay+b=0}\end{array}\right.$，解得：B（$-\frac{b}{1+2a}，-\frac{2b}{1+2a}$），
联立$\left\{\begin{array}{l}{y=-2x}\\{x+ay+b=0}\end{array}\right.$，解得：A（$-\frac{b}{1-2a}，\frac{2b}{1-2a}$），
由题意可知$\left\{\begin{array}{l}{-\frac{b}{1+2a}＞0}\\{-\frac{b}{1-2a}＞0}\end{array}\right.$，则b＜0，$-\frac{1}{2}＜a＜\frac{1}{2}$．
由z=x-y，得y=x-z，
由图可知，当直线y=x-z过A时，直线在y轴上的截距最小，z有最大值为$-\frac{b}{1-2a}-\frac{2b}{1-2a}=-\frac{3b}{1-2a}$；
当直线y=x-z过B时，直线在y轴上的截距最大，z有最小值为$-\frac{b}{1+2a}+\frac{2b}{1+2a}=\frac{b}{1+2a}$．
由M-m=1，得$-\frac{3b}{1-2a}-\frac{b}{1+2a}=1$，
∴$b=\frac{4{a}^{2}-1}{4a+4}$，
则a+b=$a+\frac{4{a}^{2}-1}{4a+4}=\frac{8{a}^{2}+4a-1}{4（a+1）}$=$2（a+1）+\frac{3}{4（a+1）}-3$，
∵$-\frac{1}{2}＜a＜\frac{1}{2}$，∴a+1∈（$\frac{1}{2}，\frac{3}{2}$），
则a+1=$\frac{\sqrt{6}}{4}$时，$（a+b）_{mn}=\sqrt{6}-3$，
当a+1→$\frac{3}{2}$时，a+b→$\frac{1}{2}$．
∴a+b的取值范围为[$\sqrt{6}$-3，$\frac{1}{2}$）．
故选：C．

点评 本题考查简单的线性规划，考查数形结合的解题思想方法，训练了利用函数的单调性求函数的最值，属难度较大的题目．