题目内容
20.函数f(x)=lg|2x-1|的对称轴为x=$\frac{1}{2}$.分析 利用函数y=lg|x|图象的对称轴为x=0,求出函数y=lg|2x-1|图象的对称轴.
解答 解:∵函数y=lg|x|图象的对称轴是x=0,
∴函数y=lg|2x-1|图象的对称轴为2x-1=0,即x=$\frac{1}{2}$.
故答案为:x=$\frac{1}{2}$.
点评 本题考查了函数对称性的应用问题,也考查了分析与解决问题的能力,是基础题目.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
10.已知实数x,y满足条件$\left\{\begin{array}{l}{4{x}^{2}-{y}^{2}≥0}\\{x+ay+b≤0}\\{x≥0}\end{array}\right.$,z=x-y的最大值、最小值分别为M、m,且M-m=1,则a+b的取值范围为( )
| A. | [$\frac{3\sqrt{3}}{2}$-2,$\frac{\sqrt{3}}{2}$) | B. | (-$\frac{1}{2}$,$\frac{1}{2}$) | C. | [$\sqrt{6}$-3,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,$\frac{23}{10}$) |
15.公差为1的等差数列{an}中,Sn为其前n项的和,若仅S9在所有的Sn中取最小值,则首项a1的取值范围为( )
| A. | [-10,-9] | B. | (-10,-9) | C. | [-9,-8] | D. | (-9,-8) |
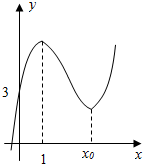 已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图.
已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图.