题目内容
【题目】已知双曲线 
﹣ 
=1（a＞0，b＞0）的左、右焦点分别是F1 ， F2 ， 过F2的直线交双曲线的右支于P，Q两点，若|PF1|=|F1F2|，且3|PF2|=2|QF2|，则该双曲线的离心率为（ ）
A.
B.
C.2
D.
【答案】A
【解析】解：如图，l为该双曲线的右准线，设P到右准线的距离为d；
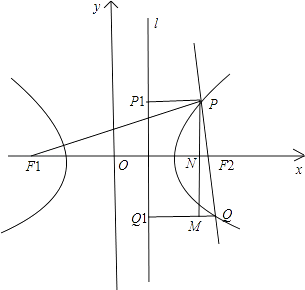
过P作PP1⊥l，QQ1⊥l，分别交l于P1，Q1；
∵ 
，3|PF2|=2|QF2|；
∴ 
， 
；
过P作PM⊥QQ1，垂直为M，交x轴于N，则：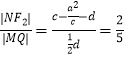 
；
∴解得d= 
；
∵根据双曲线的定义，|PF1|﹣|PF2|=2a，∴|PF2|=2c﹣2a；
∴根据双曲线的第二定义，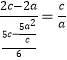 
；
整理成： 
；
∴解得 
（舍去）；
即该双曲线的离心率为 
．
故选A．
练习册系列答案
相关题目
