题目内容
【题目】已知随圆E： 
+ 
=1（a＞b＞0）与过原点的直线交于A、B两点，右焦点为F，∠AFB=120°，若△AFB的面积为4 
，则椭圆E的焦距的取值范围是（ ）
A.[2，+∞）
B.[4，+∞）
C.[2 ，+∞）
D.[4 ，+∞）
【答案】B
【解析】解：取椭圆的左焦点F1，连接AF1，BF1，
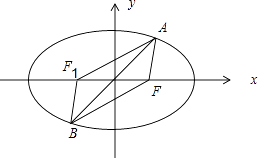
则AB与FF1互相平分，
∴四边形AFBF1是平行四边形，
∴AF1=BF，
∵AF+AF1=2a，∴AF+BF=2a，
∵S△ABF= 
AFBFsin120°= 
AFBF=4 
，
∴AFBF=16，
∵2a=AF+BF≥2 
=8，∴a≥4，
又S△ABF= 
=c|yA|=4 ，
∴c= 
，
∴当|yA|=b= 
时，c取得最小值，此时b= c，
∴a2=3c2+c2=4c2，∴2c=a，
∴2c≥4．
故选B．
练习册系列答案
相关题目
【题目】漳州水仙鳞茎硕大，箭多花繁，色美香郁，素雅娟丽，有“天下水仙数漳州”之美誉．现某水仙花雕刻师受雇每天雕刻250粒水仙花，雕刻师每雕刻一粒可赚1.2元，如果雕刻师当天超额完成任务，则超出的部分每粒多赚0.5元；如果当天未能按量完成任务，则按完成的雕刻量领取当天工资． （Ⅰ）求雕刻师当天收入（单位：元）关于雕刻量n（单位：粒，n∈N）的函数解析式f（n）；
（Ⅱ）该雕刻师记录了过去10天每天的雕刻量n（单位：粒），整理得如表：
雕刻量n | 210 | 230 | 250 | 270 | 300 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10天记录的各雕刻量的频率作为各雕刻量发生的概率．
（ⅰ）在当天的收入不低于276元的条件下，求当天雕刻量不低于270个的概率；
（ⅱ）若X表示雕刻师当天的收入（单位：元），求X的分布列和数学期望．
