题目内容
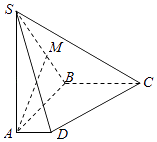
【题目】△ABC的内角A,B,C的对边分别为a,b,c,其中b≠c,且bcosB=ccosC,延长线段BC到点D,使得BC=4CD=4,∠CAD=30°, 
(Ⅰ)求证:∠BAC是直角;
(Ⅱ)求tan∠D的值.
【答案】解:(Ⅰ)证明:由正弦定理可得sinBcosB=sinCcosC,
即sin2B=sin2C,
∵b≠c,
∴2B+2C=180°,
∴B+C=90°,
∴∠BAC=180°﹣90°=90°,
(Ⅱ):如图所示:过点C做CE⊥AC,
∵BC=4,BC=4CD,
∴CD=1,BD=5,
∵∠BAC=90°,
∴CE∥AB,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
设CE=x,则AB=5x,
∵∠CAD=30°,
∴AE=2x,AC= ![]() x,
x,
∴ ![]() =
= ![]() ,
,
∴DE= ![]() x,
x,
∵AB2+AC2=BC2,
∴25x2+3x2=16,
解得x= ![]() ,
,
在△CED中,∠CED=120°,CE= ![]() ,CD=1,
,CD=1,
由正弦定理可得 ![]() =
= ![]() ,
,
即sinD= 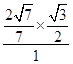 =
= ![]() ,
,
cosD= ![]() =
= ![]() ,
,
∴tanD= ![]() =
= ![]() .
.
【解析】(Ⅰ)根据正弦定理以及二倍角公式即可证明,(Ⅱ)如图所示:过点C做CE⊥AC,根据平行线分线段成比例定理,设CE=x,则AB=5x,AD= ![]() x,再根据勾股定理可得x的值,再由正弦定理,sinD=
x,再根据勾股定理可得x的值,再由正弦定理,sinD= ![]() ,再根据同角的三角函数的关系即可求出答案.
,再根据同角的三角函数的关系即可求出答案.

【题目】漳州水仙鳞茎硕大,箭多花繁,色美香郁,素雅娟丽,有“天下水仙数漳州”之美誉.现某水仙花雕刻师受雇每天雕刻250粒水仙花,雕刻师每雕刻一粒可赚1.2元,如果雕刻师当天超额完成任务,则超出的部分每粒多赚0.5元;如果当天未能按量完成任务,则按完成的雕刻量领取当天工资. (Ⅰ)求雕刻师当天收入(单位:元)关于雕刻量n(单位:粒,n∈N)的函数解析式f(n);
(Ⅱ)该雕刻师记录了过去10天每天的雕刻量n(单位:粒),整理得如表:
雕刻量n | 210 | 230 | 250 | 270 | 300 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10天记录的各雕刻量的频率作为各雕刻量发生的概率.
(ⅰ)在当天的收入不低于276元的条件下,求当天雕刻量不低于270个的概率;
(ⅱ)若X表示雕刻师当天的收入(单位:元),求X的分布列和数学期望.