Question

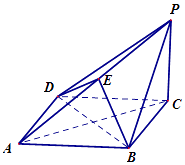
【题目】如图，矩形ABCD中，AB=2 ，AD= ，M为DC的中点，将△DAM沿AM折到△D′AM的位置，AD′⊥BM．
（1）求证：平面D′AM⊥平面ABCM；
（2）若E为D′B的中点，求二面角E﹣AM﹣D′的余弦值．

Answer 1

【答案】
（1）证明：由题知，在矩形ABCD中，∠AMD=∠BMC=45°，

∴∠AMB=90°，

又D'A⊥BM，∴BM⊥面D'AM，

∵BM面ABCM，

∴面ABCM⊥面D'AM

（2）解：由（Ⅰ）知，在平面D'AM内过M作直线NM⊥MA，则NM⊥平面ABCM，

故以M为原点， 分别为x，y，z轴的正方向建立空间直角坐标系，

则M（0，0，0），A（2，0，0），B（0，2，0），D'（1，0，1），

于是 ， ， ，

设平面EAM的法向量为 ，

则 令y=1，得平面EAM的一个法向量 ，

平面D'AM的一个法向量为 ，

故 ，

即二面角E﹣AM﹣D'的余弦值为 ．

【解析】（Ⅰ）推导出∠AMB=90°，D'A⊥BM，从而BM⊥面D'AM，由此能证明面ABCM⊥面D'AM．（Ⅱ）在平面D'AM内过M作直线NM⊥MA，以M为原点， 分别为x，y，z轴的正方向建立空间直角坐标系，利用向量法能求出二面角E﹣AM﹣D'的余弦值．
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点，需要掌握一个平面过另一个平面的垂线，则这两个平面垂直才能正确解答此题．