Question

【题目】随着旅游观念的转变和旅游业的发展，国民在旅游休闲方面的投入不断增多，民众对旅游的需求也不断提高，安庆某社区居委会统计了2011至2015年每年春节期间外出旅游的家庭数，具体统计资料如表：

年份（x）	2011	2012	2013	2014	2015
家庭数（y）	6	10	16	22	26

（1）从这5年中随机抽取两年，求外出旅游的家庭至少有1年多于20个的概率；
（2）利用所给数据，求出春节期间外出旅游的家庭数与年份之间的回归直线方程 ，并判断它们之间是正相关还是负相关；
（3）利用（2）中所求出的回归直线方程估计该社区2016年在春节期间外出旅游的家庭数．
参考公式： ， ．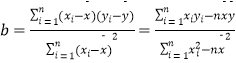

Answer 1

【答案】
（1）解：从这5年中任意抽取2年，所有的事件有：

（2011，2012），（2011，2013），（2011，2014），（2011，2015），

（2012，2013），（2012，2014）．（2012，2015），

（2013，2014），（2013，2015），（2014，2015）共10种，

外出旅游的家庭数至少有1年多于20个的事件有

（2011，2014），（2011，2015），（2012，2014），（2012，2015），

（2013，2014），（2013，2015），（2014，2015）共7种；

故概率为P=0.7；

（2）解：由已知数据计算得 =2013， =16，

=（﹣2）（﹣10）+（﹣1）（﹣6）+1×6+2×10=52，

=（﹣2）2+（﹣1）2+12+22=10，

所以 = = 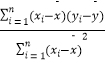=5.2，

=16﹣5.2×2013=﹣10451.6，

所以回归直线方程为y=5.2x﹣10451.6，

因为 =5.2＞0，所以外出旅游的家庭数与年份之间是正相关；

（3）解：2016年该社区在春节期间外出旅游的家庭数的估计值为

y=5.2×2016﹣10451.6≈32，

答：估计该社区2016年在春节期间外出旅游的家庭数为32

【解析】（1）利用列举法求出基本事件数，再计算对应的概率值；（2）由题目中的公式计算 、 ，求出回归系数 、 ，写出回归直线方程，由此判断是正相关还是负相关；（3）由回归方程计算x=2016时y的值即可．