��Ŀ����
����Ŀ���躯��f��x��=ax+bx��cx �� ����c��a��0��c��b��0��
��1���Ǽ���M={��a��b��c��|a��b��c���ܹ���һ�������ε������߳�����a=b}����a��b��c����M����Ӧ��f��x��������ȡֵ����Ϊ ��
��2����a��b��c�ǡ�ABC�������߳��������н�����ȷ���� �� ��д��������ȷ���۵���ţ�
��x�ʣ����ޣ�1����f��x����0��
��x��R��ʹax �� bx �� cx���ܹ���һ�������ε������߳���
������ABCΪ�۽������Σ���x�ʣ�1��2����ʹf��x��=0��
���𰸡�
��1��{x|0��x��1}
��2���٢ڢ�
���������⣺��1����Ϊc��a����a��b��c���ܹ���һ�������ε������߳���c��a+b=2a������ ![]() ����
���� ![]() ��
��
��f��x��=ax+bx��cx= ![]() ��
��
�� ![]() ������
������ ![]() ��
��
�֡� ![]() ��1����ln
��1����ln ![]() ��0������x=
��0������x= ![]() ��0��
��0��
����0��x��1��
���Դ���{x|0��x��1}��
��2������Ϊ ![]() ��
��
�� ![]() ��
��
���Զ�x�ʣ����ޣ�1���� ![]() ��
��
�����������ȷ��
����x=��1��a=2��b=4��c=5����ax= ![]() ��bx=
��bx= ![]() ��cx=
��cx= ![]() �����ܹ���һ�������ε������߳���
�����ܹ���һ�������ε������߳���
�����������ȷ��
����������Ϊ�۽������Σ���a2+b2��c2��0��
f��1��=a+b��c��0��f��2��=a2+b2��c2��0��
����x�ʣ�1��2����ʹf��x��=0��
�����������ȷ��
���Դ��Ǣ٢ڢۣ�
�����㾫����ͨ������������������ж���Ӧ�úͺ�������㣬�����������⻥Ϊ������⣬��������ͬ������ԣ���������Ϊ������������⣬���ǵ������û�й�ϵ�������������Ƿ��̵�ʵ�������༴������ͼ�����ύ��ĺ����꣮����������ʵ������������ͼ�����������н��㣬��������㼴���Խ����⣮

����Ŀ���������ι����ת�������ҵ�ķ�չ���������������з����Ͷ�벻�����࣬���ڶ����ε�����Ҳ������ߣ�����ij������ί��ͳ����2011��2015��ÿ�괺���ڼ�������εļ�ͥ��������ͳ�����������
��ݣ�x�� | 2011 | 2012 | 2013 | 2014 | 2015 |
��ͥ����y�� | 6 | 10 | 16 | 22 | 26 |
��1������5���������ȡ���꣬��������εļ�ͥ������1�����20���ĸ��ʣ�
��2�������������ݣ���������ڼ�������εļ�ͥ�������֮��Ļع�ֱ�߷��� ![]() �����ж�����֮��������ػ��Ǹ���أ�
�����ж�����֮��������ػ��Ǹ���أ�
��3�����ã�2����������Ļع�ֱ�߷��̹��Ƹ�����2016���ڴ����ڼ�������εļ�ͥ����
�ο���ʽ�� 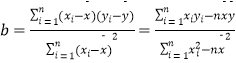 ��
�� ![]() ��
��