题目内容
【题目】某电脑公司有6名产品推销员,其工作年限与推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 3 | 4 | 5 |
(1)求年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程;
的线性回归方程;
(2)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:线性回归方程![]() 中,
中, ,
,![]() ,其中
,其中![]() 为样本平均值.
为样本平均值.
【答案】(1) ![]() .
.
(2) 5.9万元.
【解析】分析:(1)首先求出x,y的平均数,利用最小二乘法做出![]() 的值,再利用样本中心点满足线性回归方程和前面做出的横标和纵标的平均值,求出
的值,再利用样本中心点满足线性回归方程和前面做出的横标和纵标的平均值,求出![]() 的值,写出线性回归方程.
的值,写出线性回归方程.
(2)第6名推销员的工作年限为11年,即当x=11时,把自变量的值代入线性回归方程,得到y的预报值,即估计出第6名推销员的年推销金额为5.9万元.
详解:(1)设所求的线性回归方程为![]() ,
,
则 ,
,
![]() ,
,
∴年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程为
的线性回归方程为![]() ;
;
(2)当![]() 时,
时,![]() (万元).
(万元).
∴可以估计第6名推销员的年推销金额为5.9万元.

【题目】已知变量![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 之间的一组相关数据如表所示,则下列说法错误的是( )
之间的一组相关数据如表所示,则下列说法错误的是( )
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 变量![]() 之间呈现负相关关系
之间呈现负相关关系
B. ![]() 的值等于5
的值等于5
C. 变量![]() 之间的相关系数
之间的相关系数![]()
D. 由表格数据知,该回归直线必过点(9,4)
【题目】随着旅游观念的转变和旅游业的发展,国民在旅游休闲方面的投入不断增多,民众对旅游的需求也不断提高,安庆某社区居委会统计了2011至2015年每年春节期间外出旅游的家庭数,具体统计资料如表:
年份(x) | 2011 | 2012 | 2013 | 2014 | 2015 |
家庭数(y) | 6 | 10 | 16 | 22 | 26 |
(1)从这5年中随机抽取两年,求外出旅游的家庭至少有1年多于20个的概率;
(2)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程 ![]() ,并判断它们之间是正相关还是负相关;
,并判断它们之间是正相关还是负相关;
(3)利用(2)中所求出的回归直线方程估计该社区2016年在春节期间外出旅游的家庭数.
参考公式: 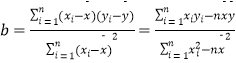 ,
, ![]() .
.
【题目】某学校为了制定治理学校门口上学、放学期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查.根据从中随机抽取的50份调查问卷,得到了如下的列联表:
同意限定区域停车 | 不同意限定区域停车 | 合计 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
则认为“是否同意限定区域停产与家长的性别有关”的把握约为__________.
附:![]() ,其中
,其中![]() .
.
| 0.050 | 0.005 | 0.001 |
| 3.841 | 7.879 | 10.828 |