题目内容
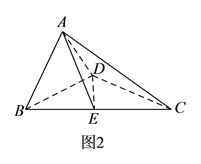
【题目】(2016·重庆高二检测)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=![]() AA1,D是棱AA1的中点.
AA1,D是棱AA1的中点.

(1)证明:平面BDC1⊥平面BDC.
(2)平面BDC1分此棱柱为两部分,求这两部分体积的比.
【答案】(1)见解析(2)1:1
【解析】试题分析:(1)由题意易证![]() 平面
平面![]() ,再由面面垂直的判定定理即可得平面
,再由面面垂直的判定定理即可得平面![]() 平面
平面![]() ;(2)设棱锥
;(2)设棱锥![]() 的体积为
的体积为![]() ,易求
,易求![]() ,三棱柱
,三棱柱![]() 的体积为
的体积为![]() ,于是可得
,于是可得![]() ,从而得到答案.
,从而得到答案.
试题解析:(1)证明:由题设知BC⊥CC1,BC⊥AC,CC1∩AC=C,
所以BC⊥平面ACC1A1.
又DC1平面ACC1A1,所以DC1⊥BC.
由题设知∠A1DC1=∠ADC=45°,
所以∠CDC1=90°,即DC1⊥DC.
又DC∩BC=C,所以DC1⊥平面BDC.
又DC1平面BDC1,故平面BDC1⊥平面BDC.
(2)设棱锥B—DACC1的体积为V1,AC=1.
由题意得V1=![]() ×
×![]() ×1×1=
×1×1=![]() .
.
又三棱柱ABC—A1B1C1的体积V=1,
所以(V-V1)∶V1=1∶1.
故平面BDC1分此棱柱所得两部分体积的比为1∶1.

练习册系列答案
相关题目